题目内容
13.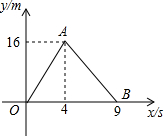 哥哥与弟弟两个人跑步,哥哥让弟弟先跑,如图所示的是两个人之间的距离y与时间x之间的函数图象,根据图中信息回答下列问题.
哥哥与弟弟两个人跑步,哥哥让弟弟先跑,如图所示的是两个人之间的距离y与时间x之间的函数图象,根据图中信息回答下列问题.(1)哥哥让弟弟先跑多少秒?哥哥出发几秒后追上了弟弟?
(2)哥哥与弟弟的速度分别是多少?
分析 (1)根据图象,两人之间的距离达到最大值的时间即为弟弟先跑的时间,根据哥哥出发后两人之间的距离变小,即可得到哥哥追上弟弟所需的时间;
(2)根据弟弟先跑4秒的路程为16米,即可得到弟弟的速度;根据哥哥出发后5秒追上弟弟,可得哥哥的速度.
解答 解:(1)由图可得,当时间为4秒时,两人之间的距离达到最大值,故哥哥让弟弟先跑4秒;
由图可得,当时间为9秒时,两人之间的距离为0,即哥哥追上弟弟,而9-4=5,
因此哥哥出发5秒后追上了弟弟;
(2)由图可得,弟弟先跑4秒的路程为16米,
故弟弟的速度为16÷4=4米/秒;
设哥哥的速度为x米/秒,根据哥哥出发后5秒追上弟弟,可得
5x-4×5=16,
解得x=7.2,
故哥哥的速度为7.2米/秒.
点评 本题主要考查了函数图象,对于一个函数,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
3.判断式子①$\frac{2x}{3+x}$和②$\frac{2}{3x}$是否分式,下面的说法正确的是( )
| A. | ①②都是 | B. | ①②都不是 | C. | ①是②不是 | D. | ①不是②是 |
1. 如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )
如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )
 如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )
如图,反比例函数y=$\frac{k}{x}$(k>0)在第一象限的一个分支与直线l交于点D丶E,直线l与x轴、y轴分别交于点M、N,点F为线段EN上的点,点G为线段DE上的点,FA⊥x轴于点A,GB⊥x轴于点B,DC⊥x轴于点C,若△OAF的面积为S1,△OBG的面积为S2,△ODC的面积为S3,则S1,S2,S3的大小关系为( )| A. | S1<S3<S2 | B. | S1<S2<S3 | C. | S2<S1<S3 | D. | S3<S1<S2 |
2.在中考体育测试时,有六个男生引体向上的成绩分别是:11、10、13、17、10、23,对于这组数据,下列说法不正确的是( )
| A. | 平均数是14 | B. | 众数是10 | C. | 中位数是15 | D. | 方差是22 |
 小明和小颖在如图所示的四边形场地上,沿边骑自行车进行场地追逐赛(两人只要有一个人回到自己的出发点,则比赛结束).小明从A地出发,沿A→B→C→D→A的路线匀速骑行,速度为8米/秒;小颖从B地出发,沿B→C→D→A→B的路线匀速骑行,速度为6米/秒.已知∠ABC=90°,AB=40米,BC=80米,CD=90米.设骑行时间为t秒,假定他们同时出发且每转一个弯需要额外耗时2秒.
小明和小颖在如图所示的四边形场地上,沿边骑自行车进行场地追逐赛(两人只要有一个人回到自己的出发点,则比赛结束).小明从A地出发,沿A→B→C→D→A的路线匀速骑行,速度为8米/秒;小颖从B地出发,沿B→C→D→A→B的路线匀速骑行,速度为6米/秒.已知∠ABC=90°,AB=40米,BC=80米,CD=90米.设骑行时间为t秒,假定他们同时出发且每转一个弯需要额外耗时2秒. 如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.
如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.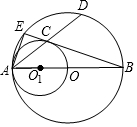 如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E.
如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E.