Question

【题目】若直线l : y kx b k 0 与曲线有 n 个交点，则称直线l 为曲线的“ n 阶共生直线”，交点称为它们的“共生点”.

（1）若直线 y kx b k 0与某曲线的一个“共生点”为 P m, 2m 1，试判断此“共生点”不可能位于第几象限，请说明理由.

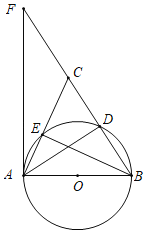
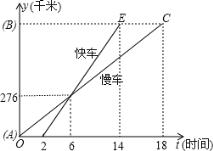
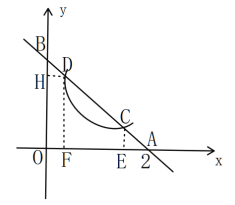
（2）若直线 l : y kx 2k k 0 与 x 、 y 轴分别交于 A 、 B 两点，且直线 l 为反比例函数y=的“ 2阶共生直线”，且“共生点”为C、D，求k的取值范围，试证明此时不论 k 取何值，总有 AC BD 成立.

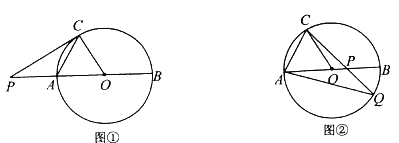
（3）若直线l : y kx 2k k 0 与 x 轴交于点 A ，且直线l 为抛物线 y x2 2x 1的“2 阶共生直线”，且“共生点”为 P 、Q xP xQ ，若 AQ 3AP ，求 k 的值.

Answer 1

【答案】（1）不经过第四象限，（2），证明见解析；（3）

【解析】

（1）直线y=2x+1不经过第四象限，故得答案；

（2）过点C作CE⊥ OA ,过点D作DF⊥OA,DH⊥OB，列方程组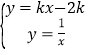整理得一个一元二次方程，由交点数可知方程有两个不相等的实数根，故△= 可求得K的取值范围，然后求得A(2,0)，设，解得，故AE=OF=DH，证得△ACE≌△DHB，得出AC=BD，所以此时不论 k 取何值，总有 AC BD 成立；

（3）作出图形，则有，列出方程解得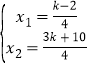，又因为，所以，求解可得k值.

解：（1）∵P（m,2m+1）在直线y=2x+1上，它不经过第四象限，

∴P不可能位于第四象限.

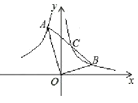
（2）如图，过点C作CE⊥ OA ,过点D作DF⊥OA,DH⊥OB，

由题意列方程组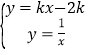，整理得，

因为有2个交点，故方程有两个不相等的实数根，

∴△=

解得

令y=0,得x=2,所以A(2,0)

设

∴

∴

∴AE=OF=DH

又∵AC,BD在同一直线上，易得△ACE≌△DHB

∴AC=BD

∴此时不论 k 取何值，总有 AC BD 成立.

（3）如图

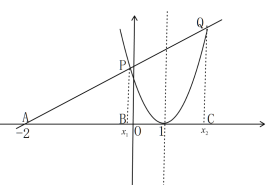
又

∴

∴

∴

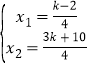
又∵

∴

∴

∴（负值舍去）

得