Question

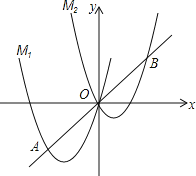
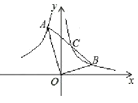
【题目】已知，如图点 A 、B 分别在反比例函数和上，OA OB ，连接 AB 与交于点C ，若C 为 AB 中点，则 SOAB =_____.

Answer 1

【答案】

【解析】

过点A作AE⊥x轴于点E，过点B作BD⊥x轴于点D，则△AOE∽△OBD，根据相似三角形的性质结合反比例函数k的几何意义可得出，得到△OBC是等边三角形，BC=OB，点B,C关于直线y=x对称，设B(m,)，则，由两点间的距离公式得到，，列出方程求解，再把所得的解代入三角形面积代数式中计算可得出.

解：过点A作AE⊥x轴于点E，过点B作BD⊥x轴于点D，

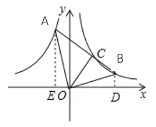
∵OA OB则易证△AOE∽△OBD

A 、B 分别在反比例函数和上，则SOAE=, SOBD=,

∴∠OBA=60°

∵C 为 AB 中点,

∴△OBC是等边三角形，BC=OB

∵关于y=x对称，

∴点B,C关于直线y=x对称

设B(m,)，则

，

∴

解得：

将代入，化简得