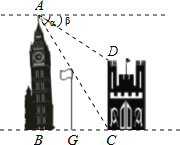
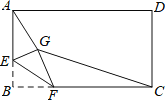
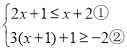题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,过点A作半圆O的切线交BC的延长线于点F,连结BE,AD
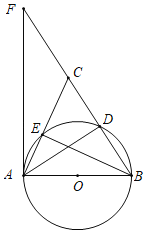
(1)求证:∠F=∠EBC;
(2)若AE=2,tan∠EAD=![]() ,求AD的长.
,求AD的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由切线的性质可得∠F+∠ABC=90°,可证得∠EBC+∠ACB=90°,由∠ACB=∠ABC,可得∠F=∠EBC;
(2)先求出CE长,则AC可求出,由勾股定理可得AD长.
(1)证明:∵AB为直径,
∴∠AEB=∠CEB=90°,即∠EBC+∠ACB=90°,
∵AF切半圆O于点A,
∴∠FAB=90°,
∴∠F+∠ABC=90°,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠F=∠EBC;
(2)解:∵∠EAD=∠CBE,
∴tan![]() ,
,
∴设CE=x,则BE=2x,AB=AC=2+x.
在Rt△AEB中,22+(2x)2=(2+x)2,
解得,x1=0(舍去),![]() .
.
∴![]() ,
,
在Rt△ACD中,CD2+AD2=AC2,
∴(![]() )
)![]() ,
,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:周一至周五英语听力训练人数统计表
年级 | 参加英语听力训练人数 | ||||
周一 | 周二 | 周三 | 周四 | 周五 | |
七年级 | 15 | 20 |
| 30 | 30 |
八年级 | 20 | 24 | 26 | 30 | 30 |
合计 | 35 | 44 | 51 | 60 | 60 |

(1)填空:![]() ________;
________;
(2)根据上述统计图表完成下表中的相关统计量:
年级 | 平均训练时间的中位数 | 参加英语听力训练人数的方差 |
七年级 | 24 | 34 |
八年级 | 14.4 |
(3)请你利用上述统计图表,对七、八年级英语听力训练情况写出两条合理的评价;
(4)请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.