题目内容
6. 如图所示,已知E为?ABCD中D边延长线上一点,且CE=DC,连AE分别交BC、BD于F、G,连AC交BD于O点,连OF.
如图所示,已知E为?ABCD中D边延长线上一点,且CE=DC,连AE分别交BC、BD于F、G,连AC交BD于O点,连OF.(1)求证:AF=EF;
(2)求证:DE=4OF.
分析 (1)由四边形ABCD是平行四边形,可得CB∥AD,根据平行线分线段成比例定理,可证得CE:DC=EF:AF,然后由CE=DC,证得结论;
(2)由四边形ABCD是平行四边形,AF=EF,易证得OF是△ACE的中位线,继而证得△BOF∽△BDC,然后由相似三角形的对应边成比例,证得CD=2OF,继而证得结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴CF∥AD,
∴CE:DC=EF:AF,
∵CE=DC,
∴AF=EF;
(2)∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AF=EF,
∴OF=$\frac{1}{2}$CE,OF∥CD,
∴△BOF∽△BDC,
∴OF:CD=OB:DB=1:2,
∴OF=$\frac{1}{2}$CD,
∴DE=CE+CD=4OF.
点评 此题考查了平行四边形的性质、三角形中位线的性质以及相似三角形的判定与性质.注意证得OF是△ACE与△BCD的中位线是关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
16.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与悬挂的物体的质量x(kg)间有下面的关系:
下列说法不正确的是( )
| 质量/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| 长度/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x和y都是变量,且x是自变量,y是因变量 | |
| B. | 弹簧不悬挂重物时的长度为0 | |
| C. | 在弹性限度内,物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 在弹性限度内,所挂物体的质量为7kg,弹簧长度为13.5cm |
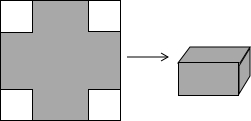 你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少.
你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少. 已知,如图,AB∥CD,∠ABE=∠DCF,BE与CF会不会平行,为什么?
已知,如图,AB∥CD,∠ABE=∠DCF,BE与CF会不会平行,为什么?