题目内容
18．在同一平面直角坐标系中，抛物线y=x2+4x=5与坐标轴的交点有3个．分析 先计算判别式的值可判断抛物线y=x2+4x=5与x轴有两个交点，再确定抛物线与y轴的交点坐标，于是可得到抛物线y=x2+4x=5与坐标轴的交点个数．
解答 解：∵△=42-4×（-5）=36＞0，
∴抛物线y=x2+4x=5与x轴有两个交点，
而抛物线与y轴的交点坐标为（0，-5），
∴抛物线y=x2+4x=5与坐标轴有3个交点．
故答案为3．
点评 本题考查了抛物线与x轴的交点：对于二次函数y=ax2+bx+c（a，b，c是常数，a≠0），△=b2-4ac决定抛物线与x轴的交点个数：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．
练习册系列答案
相关题目
10．在△ABC中，∠BAC=90°，AB=3，AC=4，D是BC的中点，则BD的长为（ ）
| A． | 5 | B． | $\frac{5}{2}$ | C． | 2 | D． | $\frac{3}{2}$ |
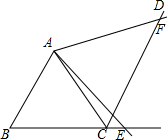已知，如图，△ABC为等边三角形，CD∥AB，点E、F分别在BC延长线及CD上，∠EAF=60°，求证：BE=CF．
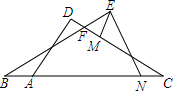已知，如图，∠EBN+∠FCA=∠MEN，AB=CN，EN=AD．EM∥AD．探究BF与CF之间的数量关系．
如图所示．点C、D在线段AB上，且点D是线段CB的中点．