题目内容
20.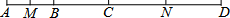 如图,AB:BC:CD=2:3:4,M是AB的中点,N是CD的中点,
如图,AB:BC:CD=2:3:4,M是AB的中点,N是CD的中点,(1)如果AB=4cm,求MN的长;
(2)如果MN=18cm,求AB的长.
分析 设AB=2xcm,BC=3xcm,CD=4xcm,
(1)由AB=4cm,求出BC,CD的长,然后再求MB,CN,再由MN=MB+BC+CN解答;
(2)求出MB=xcm,CN=2xcm,得出方程x+3x+2x=18,求出即可.
解答 解:(1)因为AB=4cm,由题意可得:BC=6cm,CD=8cm,
∵M是AB的中点,N是CD的中点,
∴MB=2cm,CN=4cm,
∴MN=MB+BC+CN=2+6+4=12cm;
(2)设AB=2xcm,BC=3xcm,CD=4xcm,
∵M是AB的中点,N是CD的中点,
∴MB=xcm,CN=2xcm,
∴MB+BC+CN=x+3x+2x=18,
∴x=3,
∴2x=6,
即AB=6cm.
点评 本题考查了求两点之间的距离的应用,关键是能根据题意得出线段之间的关系.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
1.在$\sqrt{3}$,-1,0,-$\sqrt{2}$这四个数中,最大的是( )
| A. | $\sqrt{3}$ | B. | 0 | C. | -1 | D. | -$\sqrt{2}$ |
12.已知∠AOB=65°,∠BOC=15°,则∠AOC等于( )
| A. | 80° | B. | 40° | C. | 80°或40° | D. | 以上都不对 |
10.太阳、西瓜、易拉罐、篮球、橡皮擦、书本中,形状类似圆柱的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
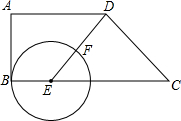 在梯形ABCD中,AD∥BC,AB⊥AD,AB=4,AD=5,CD=5.E为底边BC上一点,以点E为圆心,BE为半径画⊙E交射线ED于点F.设BE=y,DF=x.
在梯形ABCD中,AD∥BC,AB⊥AD,AB=4,AD=5,CD=5.E为底边BC上一点,以点E为圆心,BE为半径画⊙E交射线ED于点F.设BE=y,DF=x.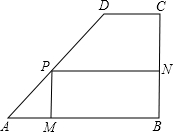 学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m
学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m 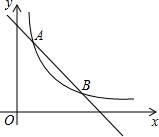 如图,在直角坐标系中,直线y=6-x与函数y=$\frac{5}{x}$(x>0)的图象交于A、B,设A(x1,y1),那么长为x1,宽为y1的矩形的面积和周长分别是5、12.
如图,在直角坐标系中,直线y=6-x与函数y=$\frac{5}{x}$(x>0)的图象交于A、B,设A(x1,y1),那么长为x1,宽为y1的矩形的面积和周长分别是5、12.