题目内容
当a+b+c=0,且ab>0,c<0时,设x=-|
+
+
|,求代数式x2013+2012x+2013的值.
| |a| |
| b+c |
| |b| |
| a+c |
| |c| |
| a+b |
考点:代数式求值,绝对值
专题:
分析:首先根据已知得出a>0,b>0,c<0,b+c=-a,a+c=-b,a+b=-c,进而代入求出x的值,即可得出答案.
解答:解:∵a+b+c=0,且ab>0,c<0,
∴a>0,b>0,c<0,b+c=-a,a+c=-b,a+b=-c,
∴x=-|
+
+
|
=-|
+
+
|
=-|-1-1+1|
=-1,
原式=x2013+2012x+2013
=(-1)2013+2012×(-1)+2013
=0.
∴a>0,b>0,c<0,b+c=-a,a+c=-b,a+b=-c,
∴x=-|
| |a| |
| b+c |
| |b| |
| a+c |
| |c| |
| a+b |
=-|
| a |
| -a |
| b |
| -b |
| -c |
| -c |
=-|-1-1+1|
=-1,
原式=x2013+2012x+2013
=(-1)2013+2012×(-1)+2013
=0.
点评:此题主要考查了代数式求值,根据已知得出x的值是解题关键.

练习册系列答案
相关题目
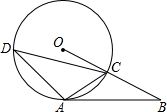 已知:如图,A是⊙O上的一点,半径OC的延长线与过点A的直径交于点B,OC=BC,AC=
已知:如图,A是⊙O上的一点,半径OC的延长线与过点A的直径交于点B,OC=BC,AC= 如图,在梯形ABCD中,AD∥BC,E是DC的中点,EF∥AB交BC于F,若EF=3,求AB的长.
如图,在梯形ABCD中,AD∥BC,E是DC的中点,EF∥AB交BC于F,若EF=3,求AB的长. 如图,AD⊥BD,BC⊥AC,AD=BC.求证:∠OAB=∠OBA.
如图,AD⊥BD,BC⊥AC,AD=BC.求证:∠OAB=∠OBA. 如图,⊙O1与⊙O2相交于A、B两点,若AB=O1A=4,O2A=2
如图,⊙O1与⊙O2相交于A、B两点,若AB=O1A=4,O2A=2