已知在△ABC中.AB=AC.DB=DC.点F是AB边上一点.点E在线段DF的延长线上.∠BAE=∠BDF.点M在线段DF上.∠EBM=∠ABD．(1)如图1.当∠ABC=45°时.求证:AE=$\sqrt{2}$MD．(2)如图2.当∠ABC=60°时.延长BM到点P.使MP=BM.AD与CP交于点N.若AB=$\sqrt{7}$.BE=$\sqrt{3}$．①求证:BP⊥CP,②求AN的� 题目和参考答案——青夏教育精英家教网—

题目内容

4．已知在△ABC中，AB=AC，DB=DC，点F是AB边上一点，点E在线段DF的延长线上，∠BAE=∠BDF，点M在线段DF上，∠EBM=∠ABD．
（1）如图1，当∠ABC=45°时，求证：AE=$\sqrt{2}$MD．
（2）如图2，当∠ABC=60°时，延长BM到点P，使MP=BM，AD与CP交于点N，若AB=$\sqrt{7}$，BE=$\sqrt{3}$．
①求证：BP⊥CP；②求AN的长．

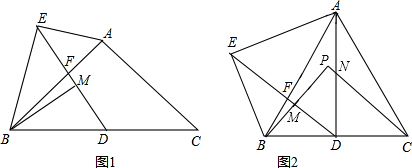
分析（1）由题意知∠BAE=∠BDM，∠ABE=∠DBM，故有△ABE∽△DBM⇒AE：DM=AB：BD，而∠ABC=45°⇒AB=$\sqrt{2}$BD，则有AE=$\sqrt{2}$MD；
（2）①由于△ABE∽△DBM，相似比为2，故有EB=2BM，由题意知得△BEP为等边三角形，有EM⊥BP，∠BMD=∠AEB=90°，由D为BC中点，M为BP中点，得DM∥PC，故∠BPC=∠BMD=90°；
②由DM∥CP得∠NCD=∠BDM=∠BAE，根据△BMD∽△BEA得∠BMD=∠BEA=90°，进而知tan∠NCD=tan∠BAE=$\frac{BE}{AE}=\frac{\sqrt{3}}{2}$，可分别求出AD、CD及DN的长，即可知AN．

解答解：（1）∵AB=AC，且∠ABC=45°，∴∠BAC=90°，
故在RT△ABC中，AB=BC•cos∠ABC=BC•cos45°，即AB=$\frac{\sqrt{2}}{2}$BC，
又∵DB=DC，∴BC=2DB，∴AB=$\sqrt{2}$DB，
∵∠EBM=∠ABD，∴∠EBA=∠MBD，
∵∠BAE=∠BDM，
∴△ABE～△DBM，∴$\frac{AB}{DB}=\frac{AE}{DM}$，
∵AB=$\sqrt{2}$DB，∴AE=$\sqrt{2}$MD；
（2）如图：

①连接AD，
∵AB=AC，∠ABC=60°，
∴△ABC是等边三角形，
又∵D为BC的中点，
∴AD⊥BC，∠DAC=30°，BD=DC=$\frac{1}{2}$AB，
∵∠BAE=∠BDM，∠ABE=∠DBM，
∴△ABE∽△DBM，
∴$\frac{BE}{BM}=\frac{AB}{DB}$=2，∠AEB=∠DMB，
∴EB=2BM，
又∵BM=MP，
∴EB=BP，
∵∠EBM=∠EBA+∠ABM=∠MBD+∠ABM=∠ABC=60°，
∴△BEP为等边三角形，
∴EM⊥BP，即∠BMD=90°，
∵DB=DC，BM=MP，
∴DM是△BCP中位线，
∴DM∥PC，
∴∠BMD=∠BPC=90°，即BP⊥PC；
②∵DM∥CP，∴∠NCD=∠BDM，
∵∠BDM=∠BAE，∴∠NCD=∠BAE，
∵△BMD∽△BEA，∠BMD=90°，
∴∠BMD=∠BEA=90°，
在RT△ABE中，AB=$\sqrt{7}$，BE=$\sqrt{3}$，∴AE=2，
则tan∠NCD=tan∠BAE=$\frac{BE}{AE}=\frac{\sqrt{3}}{2}$，
在RT△ACD中，AD=AC•sin∠ACD=$\frac{\sqrt{21}}{2}$，CD=AC•cos∠ACD=$\frac{\sqrt{7}}{2}$，
而DN=CD•tan∠NCD=$\frac{\sqrt{21}}{4}$，
∴AN=AD-DN=$\frac{\sqrt{21}}{4}$．