已知f}$.则f}$=$\frac{1}{1×2}$.f}$=$\frac{1}{2×3}$-若f=$\frac{2017}{2018}$.则n的值为2017．题目和参考答案——青夏教育精英家教网—

题目内容

12．已知f（x）=$\frac{1}{x（x+1）}$，则f（1）=$\frac{1}{1×（1+1）}$=$\frac{1}{1×2}$，f（2）=$\frac{1}{2×（2+1）}$=$\frac{1}{2×3}$…若f（1）+f（2）+f（3）+…+f（n）=$\frac{2017}{2018}$，则n的值为2017．

分析直接根据题意将原式化简进而结合分式的性质得出n的值．

解答解：∵f（1）=$\frac{1}{1×（1+1）}$=$\frac{1}{1×2}$=1-$\frac{1}{2}$，
f（2）=$\frac{1}{2×（2+1）}$=$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$…，
∴f（1）+f（2）+f（3）+…+f（n）=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{2017}{2018}$，
∴$\frac{n}{n+1}$=$\frac{2017}{2018}$，
故n=2017．
故答案为：2017．

点评此题主要考查了函数值以及分式的计算，正确将原式变形是解题关键．

练习册系列答案

相关题目

2．

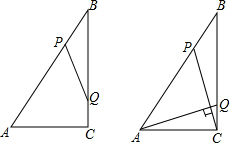如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．
（1）如图1，若△BPQ∽△BCA，求t的值；
（2）如图2，连接AQ，CP，若AQ⊥CP，求$\frac{AQ}{CP}$的值；
（3）证明：PQ的中点在△ABC的一条中位线上．

3．若不等式组$\left\{\begin{array}{l}x＞a\\ x＜b\end{array}\right.$无解（a≠b），则不等式组$\left\{\begin{array}{l}x＞2-a\\ x＜2-b\end{array}\right.$的解是2-a＜x＜2-b．

20．

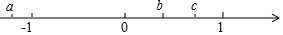在数轴上和有理数a、b、c对应的点的位置如图所示：
有下面四个结论：①abc＜0；②|a-b|+|b-c|=|a-c|③（a-b）（b-c）（c-a）＞0；④|a|＜1-bc，其中正确的结论有①②③．

7．先阅读一段文字，再回答下列问题：已知在平面内两点坐标P₁（x₁，y₁），P₂（x₂，y₂），其两点间距离公式为P₁P₂=$\sqrt{{{（{{x_2}-{x_1}}）}^2}+{{（{{y_2}-{y_1}}）}^2}}$，同时，当两点所在直线在坐标轴上或平行于x轴或垂直于x轴时，两点间距离公式可化简为|x₂-x₁|或|y₂-y₁|．
（1）已知A（3，5）、B（-2，-1），则A，B两点间的距离为$\sqrt{61}$；
（2）已知A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为-1，则A，B两点间的距离为6；
（3）已知一个三角形各顶点坐标为A（0，6），B（-3，2），C（3，2），请判定此三角形的形状，并说明理由．

17．绝对值等于$\sqrt{5}$的数是$±\sqrt{5}$；1-$\sqrt{2}$的相反数是$\sqrt{2}$-1．绝对值是$\sqrt{2}$-1．

4．下列说法正确的是（　　）

	A．	0除以任何数都得0
	B．	若a＜-1，则$\frac{1}{a}$＜a
	C．	同号两数相除，取原来的符号，并把两数的绝对值相除
	D．	若0＜a＜1，则$\frac{1}{a}$＞a

1．

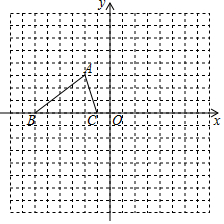如图，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）．
（1）尺规作图；在y轴上确定一个点P，使PA=PB（要求保留作图痕迹）；
（2）请以A、B、C为其中三个顶点画平行四边形（只需画一个即可）；
（3）将△ABC绕坐标原点O顺时针旋转90°，画出图形，直接写出点A的对应点的坐标．

2．

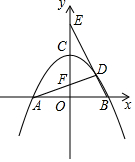如图，已知抛物线y=ax²+4（a≠0）与x轴交于点A和点B（2，0），与y轴交于点C，点D是抛物线在第一象限的点．
（1）当△ABD的面积为4时，
①求点D的坐标；
②联结OD，点M是抛物线上的点，且∠MDO=∠BOD，求点M的坐标；
（2）直线BD、AD分别与y轴交于点E、F，那么OE+OF的值是否变化，请说明理由．

试题分类