题目内容
9.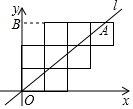 八个边长为1的正方形如图所示的位置摆放在平面直角坐标系中,经过原点的直线l将这八个正方形分成面积相等的两部分,则这条直线的解析式是y=$\frac{9}{10}$x.
八个边长为1的正方形如图所示的位置摆放在平面直角坐标系中,经过原点的直线l将这八个正方形分成面积相等的两部分,则这条直线的解析式是y=$\frac{9}{10}$x.
分析 设直线l和八个正方形的最上面交点为A,过点A作AB⊥y轴于点B,过点A作AC⊥x轴于点C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标,再利用待定系数法可求出该直线l的解析式.
解答 解:设直线l和八个正方形的最上面交点为A,过点A作AB⊥y轴于点B,过点A作AC⊥x轴于点C,如图所示.
∵正方形的边长为1,
∴OB=3.
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴$\frac{1}{2}$OB•AB=5,
∴AB=$\frac{10}{3}$,
∴OC=$\frac{10}{3}$,
∴点A的坐标为($\frac{10}{3}$,3).
设直线l的解析式为y=kx,
∵点A($\frac{10}{3}$,3)在直线l上,
∴3=$\frac{10}{3}$k,
解得:k=$\frac{9}{10}$,
∴直线l解析式为y=$\frac{9}{10}$x.
故答案为:y=$\frac{9}{10}$x.
点评 本题考查了待定系数法求一次函数解析式、正方形的性质以及三角形的面积,利用三角形的面积公式和已知条件求出A的坐标是解题的关键.

练习册系列答案
相关题目
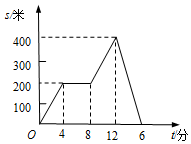 小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.
小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.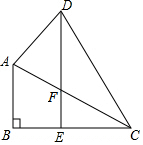 如图,在四边形ABCD中,∠B=90°,过点D作DE∥AB,交BC于E,且DE=BC,连接AC交AC于F,若∠ACB=∠CDE=30°,则图中有几个等腰三角形?请找出来并说明理由.
如图,在四边形ABCD中,∠B=90°,过点D作DE∥AB,交BC于E,且DE=BC,连接AC交AC于F,若∠ACB=∠CDE=30°,则图中有几个等腰三角形?请找出来并说明理由.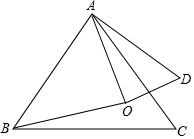 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,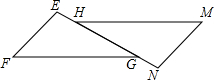 如图,△EFG≌△NMH,∠F和∠M是对应角.在△NMH中,MH是最长边.在△EFG中,FG是最长边,EF=2.1cm,EH=1.2cm,NH=4.4cm.
如图,△EFG≌△NMH,∠F和∠M是对应角.在△NMH中,MH是最长边.在△EFG中,FG是最长边,EF=2.1cm,EH=1.2cm,NH=4.4cm.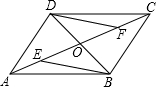 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.