题目内容
 如图,在平面直角坐标系中,直线l是一次函数,点M(2,5)的关于直线l的对称点为M′,求点M′的坐标.
如图,在平面直角坐标系中,直线l是一次函数,点M(2,5)的关于直线l的对称点为M′,求点M′的坐标.考点:坐标与图形变化-对称
专题:计算题
分析:分别过点M、M′作l的平行线,分别交y轴于A、B点,直线l交y轴于C点,连结CM、CM′,如图,利用两直线平行的问题,可设直线MA的解析式为y=
x+b,把M(2,5)代入可解得b=4,则得到A(0,4),加上C(0,3),则AC=1,再利用对称的性质得所以AC=BC=1,CM=CM′,所以B点坐标为(0,2),易得直线BM′的解析式为y=
x+2,设M′(t,
t+2),根据两点的距离公式得到22+(5-3)2=t2+(
t+2-3)2,整理得5t2-4t-28=0,解得t1=
,t2=-2(舍去),于是可得M′点的坐标.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 14 |
| 5 |
解答:解:分别过点M、M′作l的平行线,分别交y轴于A、B点,直线l交y轴于C点,连结CM、CM′,如图,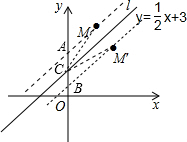
设直线MA的解析式为y=
x+b,
把M(2,5)代入得1+b=5,解得b=4,
所以直线MA的解析式为y=
x+4,则A(0,4),
而C(0,3),则AC=1,
由于点M的关于直线l的对称点为M′,
所以AC=BC=1,CM=CM′,
所以B点坐标为(0,2),则直线BM′的解析式为y=
x+2,
设M′(t,
t+2),
由于CM=CM′得22+(5-3)2=t2+(
t+2-3)2,
整理得5t2-4t-28=0,解得t1=
,t2=-2(舍去),
所以点M′的坐标为(
,
).

设直线MA的解析式为y=
| 1 |
| 2 |
把M(2,5)代入得1+b=5,解得b=4,
所以直线MA的解析式为y=
| 1 |
| 2 |
而C(0,3),则AC=1,
由于点M的关于直线l的对称点为M′,
所以AC=BC=1,CM=CM′,
所以B点坐标为(0,2),则直线BM′的解析式为y=
| 1 |
| 2 |
设M′(t,
| 1 |
| 2 |
由于CM=CM′得22+(5-3)2=t2+(
| 1 |
| 2 |
整理得5t2-4t-28=0,解得t1=
| 14 |
| 5 |
所以点M′的坐标为(
| 14 |
| 5 |
| 17 |
| 5 |
点评:本题考查了坐标与图形变化-对称:关于x轴对称,横坐标相等,纵坐标互为相反数;关于y轴对称,纵坐标相等,横坐标互为相反数.也考查了两直线平行的问题和两点间的距离公式.

练习册系列答案
相关题目
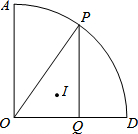 如图,扇形AOD中,∠AOD=90°,OA=6,点P为弧AD上任意一点(不与点A和D重合),PQ⊥OD于Q,点I为△OPQ的内心,过O,I和D三点的圆的半径为r.则当点P
如图,扇形AOD中,∠AOD=90°,OA=6,点P为弧AD上任意一点(不与点A和D重合),PQ⊥OD于Q,点I为△OPQ的内心,过O,I和D三点的圆的半径为r.则当点P在弧AD上运动时,r的值满足( )
| A、0<r<3 | ||
| B、r=3 | ||
C、3<r<3
| ||
D、r=3
|
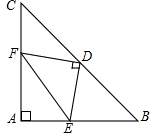 如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.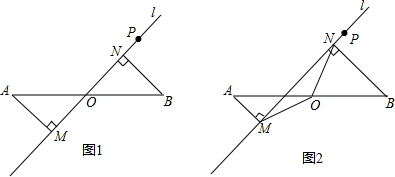
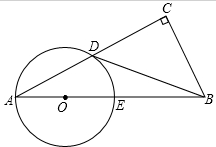 如图,在Rt△ABC中,∠C=90°,点D是AC上一点,过点A、D两点作⊙O.使圆心O在AB上,⊙O与AB交于点E,若BD为⊙O的切线,tan∠CBD=
如图,在Rt△ABC中,∠C=90°,点D是AC上一点,过点A、D两点作⊙O.使圆心O在AB上,⊙O与AB交于点E,若BD为⊙O的切线,tan∠CBD= 如图所示,D是AB的中点,E是BC的中点,BE=
如图所示,D是AB的中点,E是BC的中点,BE=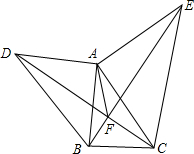 如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DC、BE交于F点.
如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DC、BE交于F点. 在菱形ABCD中,∠BAF=∠DAE,求证:BD∥EF.
在菱形ABCD中,∠BAF=∠DAE,求证:BD∥EF.