题目内容
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s,过点P作PE∥AC交DC于点E.同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,连接PQ,QE,PQ与AC交与点F,设运动时间为t(s)(0<t<8).
(1)当t为何值时,四边形PFCE是平行四边形;
(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;
(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的
 ;
;
(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.


解:(1)PD=8﹣t,CQ=2t,根据题意得:8﹣t=2t,解得:t=
 ;
;
(2)S四边形PDCQ=
 (PD+CQ)•CD=
(PD+CQ)•CD=
 ×6(8﹣t+2t)=3(8+t)=3t+24,
×6(8﹣t+2t)=3(8+t)=3t+24,
∵PE∥AC,∴
 ,∴
,∴
 =
=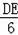
 ,则DE=﹣
,则DE=﹣
 t+6,则EC=6﹣(﹣
t+6,则EC=6﹣(﹣
 t+6)=
t+6)=
 t,
t,
则S△PDE=
 PD•DE=
PD•DE=
 (8﹣t)•(﹣
(8﹣t)•(﹣
 t+6),S△CQE=
t+6),S△CQE=
 CQ•EC=
CQ•EC=
 ×2t•
×2t•
 t=
t=
 t2,
t2,
则s=3t+24﹣
 (8﹣t)•(﹣
(8﹣t)•(﹣
 t+6)﹣
t+6)﹣
 t2,即s=﹣
t2,即s=﹣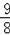
 t2+3t;
t2+3t;
(3)S矩形ABCD=6×8=48,根据由题意得:﹣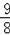
 t2+3t=
t2+3t=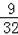
 ×48,解得:t=2或6;
×48,解得:t=2或6;
(4)在直角△PDE中,PD2=(8﹣t)2+(﹣
 t+6)2,
t+6)2,
在直角△COQ中,QE2=(2t)2+(
 t)2,
t)2,
当点E在线段PQ的垂直平分线上时,PD2=QE2,
则(8﹣t)2+(﹣
 t+6)2=(2t)2+(
t+6)2=(2t)2+(
 t)2,
t)2,
解得:t=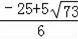
 或
或
 (舍去).则t=
(舍去).则t=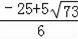
 .
.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
 ,
, ,D为BC边延长线上一点,BM平分
,D为BC边延长线上一点,BM平分 ,E
,E 为射线BM上一点.
为射线BM上一点. 的度数;
的度数; ,求
,求 (2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
 (m为常数)是一个完全平方式,则m的值为 .
(m为常数)是一个完全平方式,则m的值为 . 能被( )整除.
能被( )整除.
 ,并写出它的非负整数解.
,并写出它的非负整数解.
