题目内容
如图在梯形ABCD中AB=CD=5，AD=7，BC=13，E点在AD上，且AE=4，动点P从D出发沿着梯形的周界依次经过C、B最后到达A，设此过程中P点走过的距离为x，△APE的面积为y，把y表示成x的函数，并且画出图象．
解：这道题可以分三种情况讨论：
①当P在CD上时，0≤x≤5，过点P作PH⊥AD交AD的延长线与H，过点D作DM⊥BC交BC与点M，
已知AD=7，BC=13，易知：MC=
=3，
又AB=CD=5，根据勾股定理可得DM=4，
∵AD∥BC，
∴∠PDH=∠C，
∴PH=PD•sin∠C=x•sin∠C=
=
x，
∴y=
AE•PH=
x．
②当P在BC上时，5≤x≤18，y=•AE•DM=8，
③当P在AB上时，18≤x≤23，AP=（AB+BC+CD）-x=23-x，
由①同理可得：y=×4×（23-x）×sin∠C=
（184-8x）．
所以y=，
，
综上得所求的函数图象为：
分析：此题分三种情况：①当P在CD上时，②当P在BC上时，③当P在AB上时，分别求出解析式，根据解析式画出图象即可．
点评：本题考查了动点问题的函数图象，解题关键是对等腰梯形及三角形面积公式的熟练运用，难度适中，注意要分三种情况：P在CD上、P在BC上和P在AB上进行讨论．
①当P在CD上时，0≤x≤5，过点P作PH⊥AD交AD的延长线与H，过点D作DM⊥BC交BC与点M，
已知AD=7，BC=13，易知：MC=
=3，又AB=CD=5，根据勾股定理可得DM=4，
∵AD∥BC，
∴∠PDH=∠C，
∴PH=PD•sin∠C=x•sin∠C=
=x，∴y=
AE•PH=x．②当P在BC上时，5≤x≤18，y=
•AE•DM=8，③当P在AB上时，18≤x≤23，AP=（AB+BC+CD）-x=23-x，
由①同理可得：y=
×4×（23-x）×sin∠C=（184-8x）．所以y=，
，综上得所求的函数图象为：
分析：此题分三种情况：①当P在CD上时，②当P在BC上时，③当P在AB上时，分别求出解析式，根据解析式画出图象即可．
点评：本题考查了动点问题的函数图象，解题关键是对等腰梯形及三角形面积公式的熟练运用，难度适中，注意要分三种情况：P在CD上、P在BC上和P在AB上进行讨论．
练习册系列答案
相关题目
如图在梯形ABCD中，AB=DC=10cm，AC与BD相交于G，且∠AGD=60°，设E为CG的中点，F为AB的中点，则EF的长为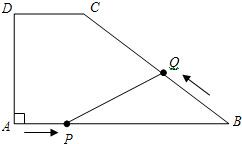
发以3厘米/秒的速度沿B?C?D方向向点D运动，两个动点同时出发，当其中一个动点到达终点时，另一个动点也随之停止．设动点运动的时间为t秒．
如图在梯形ABCD中，AD∥BC，E是梯形内一点，ED⊥AD，∠EBC=∠EDC，∠ECB=45°．
（2011•宣城模拟）我们知道连接三角形两边中点的线段叫做三角形的中位线；通过证明可以得到“三角形的中位线平行于三角形的第三边，且等于第三边的一半”类似三角形中位线，我们把连接梯形两腰中点的线段叫做梯形的中位线．如图在梯形ABCD中，AD∥BC，点E，F分别是AB、CD的中点，观察EF的位置，联想三角形中位线的性质，你能发现梯形的中位线有什么性质？证明你的结论．
如图在梯形ABCD中，AD∥BC，∠B=∠C，DE交BC于点E，AD=BE．