题目内容
已知抛物线y=ax2+bx与x轴交于点B (-4,0),顶点为(A-2,-4);连接AB,把AB所在直线沿y轴上下平移的直线设为l:y=kx+m.
(1)求抛物线的解析式;
(2)当直线l经过原点时,试在l上找一点P,使四边形BAOP为直角梯形,求出点P坐标;
(3)直线l在上下平移过程中是否存在x的取值范围,使y=ax2+bx与y=kx+m都随x的增大而减小?若存在请求出其范围,若不存在请说明理由.
(1)求抛物线的解析式;
(2)当直线l经过原点时,试在l上找一点P,使四边形BAOP为直角梯形,求出点P坐标;
(3)直线l在上下平移过程中是否存在x的取值范围,使y=ax2+bx与y=kx+m都随x的增大而减小?若存在请求出其范围,若不存在请说明理由.
考点:二次函数综合题
专题:压轴题
分析:(1)设抛物线顶点式解析式y=a(x+2)2-4,把点B的坐标代入求出a,即可得解;
(2)设直线AB的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式求出直线AB的解析式,再根据平移得到平移后的直线解析式,过点P作BP⊥OP于P,根据直线解析式设点P(a,-2a),利用勾股定理表示出列出方程求解即可;
(3)根据一次函数的增减性和二次函数的增减性解答即可.
(2)设直线AB的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式求出直线AB的解析式,再根据平移得到平移后的直线解析式,过点P作BP⊥OP于P,根据直线解析式设点P(a,-2a),利用勾股定理表示出列出方程求解即可;
(3)根据一次函数的增减性和二次函数的增减性解答即可.
解答:解:(1)设y=a(x+2)2-4,
∵过点B(-4,0),
∴(-4+2)2-4=0,
解得a=1,
∴y=(x+2)2-4;
(2)如图,∵直线y=kx+m经过点A(-2,-4),B(-4,0),
∴
,
解得
,
∴直线AB的解析式为y=-2x-8,
∴平移后过原点的直线为y=-2x,
∵四边形BAOP为直角梯形,
∴过点B作BP⊥OP,设P(a,-2a),
∵BP⊥OP,
∴OP2+BP2=BO2,
∴(a2+4a2)+(a+4)2+4a2=16,
整理得,5a2+4a=0,
解得a1=-
,a2=0(舍去),
所以,点P的坐标为(-
,
);
(3)∵y=kx+m在平移过程中k=-2始终保持不变,
∴当x为任意实数时,y都随x的增大而减小,
∵y=ax2+bx即y=(x+2)2-4,当x≤-2时,y都随x的增大而减小,
∴当x≤-2时,y=kx+m与y=ax2+bx的y值都随x的增大而减小.
∵过点B(-4,0),
∴(-4+2)2-4=0,
解得a=1,
∴y=(x+2)2-4;
(2)如图,∵直线y=kx+m经过点A(-2,-4),B(-4,0),
∴
|
解得
|
∴直线AB的解析式为y=-2x-8,
∴平移后过原点的直线为y=-2x,

∵四边形BAOP为直角梯形,
∴过点B作BP⊥OP,设P(a,-2a),
∵BP⊥OP,
∴OP2+BP2=BO2,
∴(a2+4a2)+(a+4)2+4a2=16,
整理得,5a2+4a=0,
解得a1=-
| 4 |
| 5 |
所以,点P的坐标为(-
| 4 |
| 5 |
| 8 |
| 5 |
(3)∵y=kx+m在平移过程中k=-2始终保持不变,
∴当x为任意实数时,y都随x的增大而减小,
∵y=ax2+bx即y=(x+2)2-4,当x≤-2时,y都随x的增大而减小,
∴当x≤-2时,y=kx+m与y=ax2+bx的y值都随x的增大而减小.
点评:本题是二次函数综合题,主要利用了待定系数法求函数解析式,待定系数法求一次函数解析式,勾股定理,二次函数与一次函数的增减性,难点在于(2)利用勾股定理列出方程,作出图形更形象直观.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
若x=-1是关于x的一元二次方程ax2+bx-2=0(a≠0)的一个根,则2014-2a+2b的值等于( )
| A、2014 | B、2010 |
| C、2018 | D、2012 |
 如图,几何体的俯视图是( )
如图,几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
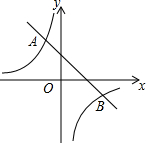 如图,一次函数y=-2x+b(b为常数)的图象与反比例函数y=
如图,一次函数y=-2x+b(b为常数)的图象与反比例函数y=