题目内容
已知直线y1=-x+1与y2=2x-2交于点P,它们与y轴分别交于点A、B.
(1)同一坐标系中画出这两个函数的图象;
(2)求出这两个函数图象的交点坐标;
(3)观察图象,当x取什么范围时,y1>y2,y1=y2,y1<y2?
(4)求△ABP的面积.
(1)同一坐标系中画出这两个函数的图象;
(2)求出这两个函数图象的交点坐标;
(3)观察图象,当x取什么范围时,y1>y2,y1=y2,y1<y2?
(4)求△ABP的面积.
考点:一次函数的图象,一次函数的性质,两条直线相交或平行问题
专题:
分析:(1)根据函数解析式得到直线与坐标轴的交点坐标,然后利用“两点确定一条直线”作出函数图象;
(2)交点坐标均满足两个函数解析式;
(3)根据函数图象直接回答问题;
(4)由点的坐标求得相关线段的长度,然后由三角形的面积公式进行解答.
(2)交点坐标均满足两个函数解析式;
(3)根据函数图象直接回答问题;
(4)由点的坐标求得相关线段的长度,然后由三角形的面积公式进行解答.
解答:解:(1)∵当x=0时,y1=1.y1=0时,x=1.
∴直线y1=-x+1经过点(0,1),(1,0).
同理,y2=2x-2经过点(0,-2),(1,0).
则其图象如图所示:
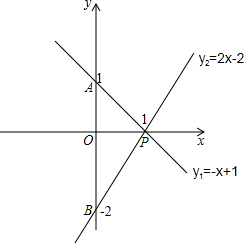 ;
;
(2)由(1)中的两直线图象知,这两个函数图象的交点坐标是(1,0);
(3)由(1)中的两直线图象知,当<1时,y1>y2;当x=1时,y1=y2,当x>1时,y1<y2;
(4)∵A(0,1),P(1,0).B(0,-2),
∴AB=3,OP=1,
∴△ABP的面积是:
AB•OP=
×3×1=
.
∴直线y1=-x+1经过点(0,1),(1,0).
同理,y2=2x-2经过点(0,-2),(1,0).
则其图象如图所示:
 ;
;(2)由(1)中的两直线图象知,这两个函数图象的交点坐标是(1,0);
(3)由(1)中的两直线图象知,当<1时,y1>y2;当x=1时,y1=y2,当x>1时,y1<y2;
(4)∵A(0,1),P(1,0).B(0,-2),
∴AB=3,OP=1,
∴△ABP的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了一次函数的图象与性质,以及两条直线相交或平行的问题.解题时,利用了“数形结合”的数学思想,使问题变得直观化,且减少了繁琐的数学计算过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AF、CF分别平分△ABC的两个外角∠DAC、∠ECA,BF平分∠ABC.求证:BF,CF,AF交于点F.(三角形的一个内角平分线与其不相邻的两个外角的平分线交于一点)
如图,AF、CF分别平分△ABC的两个外角∠DAC、∠ECA,BF平分∠ABC.求证:BF,CF,AF交于点F.(三角形的一个内角平分线与其不相邻的两个外角的平分线交于一点) 如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,且满足BE⊥AC;F为AB上一点,且CF⊥AD于H,下列判断:
如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,且满足BE⊥AC;F为AB上一点,且CF⊥AD于H,下列判断: 如图,AC⊥BC,DE⊥AC,CD⊥AB,∠1=∠2,试说明GF⊥AB.
如图,AC⊥BC,DE⊥AC,CD⊥AB,∠1=∠2,试说明GF⊥AB.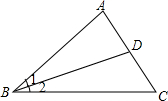 如图,下列说法:①∠1就是∠ABC;②∠2就是∠DBC;③以B为顶点的角有3个,他们是∠1,∠2,∠ABC;④∠ADB也可以表示成∠D,⑤∠BCD也可以表示成∠ACB,还可以表示成∠C,其中说法正确的有( )
如图,下列说法:①∠1就是∠ABC;②∠2就是∠DBC;③以B为顶点的角有3个,他们是∠1,∠2,∠ABC;④∠ADB也可以表示成∠D,⑤∠BCD也可以表示成∠ACB,还可以表示成∠C,其中说法正确的有( )