题目内容
如图,在直角三角形纸片上进行如下设计,直角三角形的两直角边与展开图左下角的正方形边重合,斜边恰好经过两个正方形的顶点,已知BC=36,则这个展开图围成的正方体的棱长为 .
【答案】分析:首先设这个展开图围成的正方体的棱长为x,可得EG=x,ED=3x,FG=3x,BD=x,CD=BC-BD=36-x,易证得△EFG∽△ECD,然后由相似三角形的对应边成比例,可得方程 =
= ,解此方程即可求得答案.
,解此方程即可求得答案.
解答: 解:如图,设这个展开图围成的正方体的棱长为x,
解:如图,设这个展开图围成的正方体的棱长为x,
则EG=x,ED=3x,FG=3x,BD=x,
∵BC=36,
∴CD=BC-BD=36-x,
∵FG∥BC,
∴△EFG∽△ECD,
∴ =
= ,
,
即 =
= ,
,
解得:x= .
.
故答案为: .
.
点评:此题考查了相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.
 =
= ,解此方程即可求得答案.
,解此方程即可求得答案.解答:
 解:如图,设这个展开图围成的正方体的棱长为x,
解:如图,设这个展开图围成的正方体的棱长为x,则EG=x,ED=3x,FG=3x,BD=x,
∵BC=36,
∴CD=BC-BD=36-x,
∵FG∥BC,
∴△EFG∽△ECD,
∴
 =
= ,
,即
 =
= ,
,解得:x=
 .
.故答案为:
 .
.点评:此题考查了相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•襄阳)在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是
(2013•襄阳)在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( )
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( ) 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为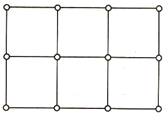 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为________.
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为________.