题目内容
 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为50
50
.分析:如图,先得到AC=BC=1,AB=
ACCD=
=
,然后进行分类讨论:如等腰直角三角形ACB的边长为1,每个小方格可得到4个这样的三角形,则这样的三角形的个数为6×4=24个;如等腰直角三角形ABE的边长为
,每两个相邻的小方格可得到4个这样的三角形,则这样的三角形的个数为7×2=14个;如等腰直角三角形DHE的边长为2,每四个小方格组成的大正方形可得到4个这样的三角形,则这样的三角形的个数为2×4=8个;如等腰直角三角形ACB的边长为
,矩形方格纸上上下两边各有两个满足条件的三角形的直角顶点,则这样的三角形的个数为4个,然后把它们相加即可.
| 2 |
| AC2+AD2 |
| 5 |
| 2 |
| 5 |
解答:解:如图,AC=BC=1,AB=
AC, CD=
CD=
=
,
当等腰直角三角形的直角边长为1时(如等腰直角三角形ACB),这样的三角形的个数为6×4=24个;
当等腰直角三角形的直角边长为
时(如等腰直角三角形ABE),这样的三角形的个数为7×2=14个;
当等腰直角三角形的直角边长为2时(如等腰直角三角形DHE),这样的三角形的个数为2×4=8个;
当等腰直角三角形的直角边长为
时(如等腰直角三角形ACB),这样的三角形的个数为4个,
所以满足条件的等腰直角三角形的个数为24+14+8+4=50.
故答案为50.
| 2 |
 CD=
CD=| AC2+AD2 |
| 5 |
当等腰直角三角形的直角边长为1时(如等腰直角三角形ACB),这样的三角形的个数为6×4=24个;
当等腰直角三角形的直角边长为
| 2 |
当等腰直角三角形的直角边长为2时(如等腰直角三角形DHE),这样的三角形的个数为2×4=8个;
当等腰直角三角形的直角边长为
| 5 |
所以满足条件的等腰直角三角形的个数为24+14+8+4=50.
故答案为50.
点评:本题考查了等腰直角三角形的性质:等腰直角三角形的两底角都为45°,斜边上的高平分斜边,并且等于斜边的一半;斜边为直角边的
倍.
| 2 |

练习册系列答案
相关题目
 7、三国时期的数学家赵爽,在其所著的《勾股圆方图注》中记载用图形的方法来解一元二次方程,四个相等的矩形(每一个矩形的面积都是35)拼成如图所示的一个大正方形,利用所给的数据,能得到的方程是( )
7、三国时期的数学家赵爽,在其所著的《勾股圆方图注》中记载用图形的方法来解一元二次方程,四个相等的矩形(每一个矩形的面积都是35)拼成如图所示的一个大正方形,利用所给的数据,能得到的方程是( )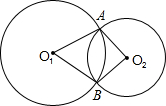 如图,⊙O1与⊙O2相交于点A、B,顺次连接O1、A、O2、B四点,得四边形O1AO2B.
如图,⊙O1与⊙O2相交于点A、B,顺次连接O1、A、O2、B四点,得四边形O1AO2B.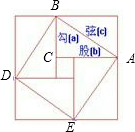 给出下列命题:①反比例函数
给出下列命题:①反比例函数




 的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )
的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(如图);④在同圆或等圆中,相等的弧所对的圆周角相等.其中正确的是( )