题目内容
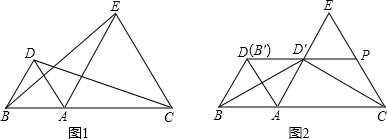
 (2013•襄阳)在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是
(2013•襄阳)在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是6
或2
| 2 |
| 13 |
6
或2
.| 2 |
| 13 |
分析:先根据题意画出图形,此题要分两种情况,再根据勾股定理求出斜边上的中线,最后根据直角三角形中,斜边上的中线等于斜边的一半即可求出斜边的长.
解答:解:①如图所示:
 ,
,
连接CD,
CD=
=
,
∵D为AB中点,
∴AB=2CD=2
;
②如图所示:
 ,
,
连接EF,
EF=
=3
,
∵E为AB中点,
∴AB=2EF=6
,
故答案为:6
或2
.
 ,
,连接CD,
CD=
| 22+32 |
| 13 |
∵D为AB中点,
∴AB=2CD=2
| 13 |
②如图所示:
 ,
,连接EF,
EF=
| 32+32 |
| 2 |
∵E为AB中点,
∴AB=2EF=6
| 2 |
故答案为:6
| 2 |
| 13 |
点评:此题考查了图形的剪拼,解题的关键是能够根据题意画出图形,在解题时要注意分两种情况画图,不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目