题目内容
2.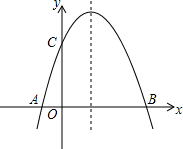 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,那个说明理由.
分析 (1)解一元二次方程x2-4x-12=0,求出点A和点B的横坐标,进而得到答案;
(2)将A、B两点坐标代入二次函数y=ax2+bx+6,得到a和b的二元一次方程组,求出a和b的值即可,进而求出顶点坐标;
(3)作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,求出C′坐标,求出直线AC′解析式,进而求出点P的坐标.
解答 解:(1)解方程x2-4x-12=0得x1=-2,x2=6,
即A(-2,0),B(6,0);
(2)将A、B两点坐标代入二次函数y=ax2+bx+6,
得到$\left\{\begin{array}{l}{4a-2b+6=0}\\{36a+6b+6=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
即y=-$\frac{1}{2}$x2+2x+6,
由于y=-$\frac{1}{2}$x2+2x+6=$\frac{1}{2}$(x-2)2+8,
即抛物线的对称轴为x=2,顶点坐标为(2,8);
(3)如图,作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,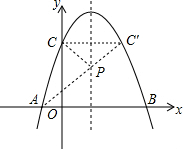
∵C(0,6),
∴C′(4,6),
设直线AC′解析式为y=kx+n,
则$\left\{\begin{array}{l}{-2k+n=0}\\{4k+n=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{n=2}\end{array}\right.$,
∴y=x+2,
当x=2时,y=4,
即P(2,4).
点评 本题主考查了二次函数的综合题,此题涉及到待定系数法求二次函数解析式和一次函数解析式、解一元二次方程以及轴对称轴的性质,解答本题的关键是作出点C关于抛物线对称轴的对称点C′,此题难度不大.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | 2a-b | B. | -2a+b | C. | -2a-b | D. | a+2b |
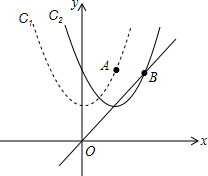 如图,已知抛物线C1:y=$\frac{1}{2}$x2+2上有一点A,点A的横坐标为2.将抛物线C1向右平移,使其顶点落在直线y=x上,此时抛物线记作为C2,点A的对应点记作B.
如图,已知抛物线C1:y=$\frac{1}{2}$x2+2上有一点A,点A的横坐标为2.将抛物线C1向右平移,使其顶点落在直线y=x上,此时抛物线记作为C2,点A的对应点记作B.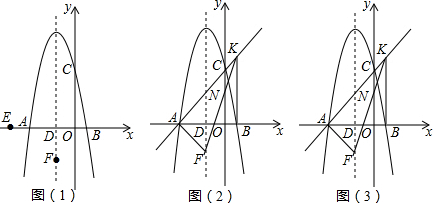
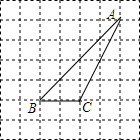 在如图所示的方格纸中,每个小正方形方格的边长都为1,△ABC的三个顶点在格点上.
在如图所示的方格纸中,每个小正方形方格的边长都为1,△ABC的三个顶点在格点上. 如图,AF=DC,BC∥EF,若添加条件∠A=∠D,则可利用“ASA”说明△ABC≌△DEF.
如图,AF=DC,BC∥EF,若添加条件∠A=∠D,则可利用“ASA”说明△ABC≌△DEF.