题目内容
如图，一架25分米的梯子，斜立在一竖直的墙上，这时梯的底部距墙底端7分米，如果梯子的顶端沿墙下滑4分米，那么梯的底部将平滑多少？考点：勾股定理的应用
专题：
分析：先利用勾股定理计算出墙高，当梯子的顶端沿墙下滑4分米后，也形成一直角三角形，解此三角形可计算梯的底部距墙底端的距离，则可计算梯子的底部平滑的距离．
解答：解：墙高为：
=24分米
当梯子的顶端沿墙下滑4分米时：则梯子的顶部距离墙底端：24-4=20分米
梯子的底部距离墙底端：
=15分米，则梯的底部将平滑：15-7=8分米．
故梯的底部将平滑8分米．
| 252-72 |
当梯子的顶端沿墙下滑4分米时：则梯子的顶部距离墙底端：24-4=20分米
梯子的底部距离墙底端：
| 252-202 |
故梯的底部将平滑8分米．
点评：本题考查正确运用勾股定理．善于观察题目的信息是解题以及学好数学的关键．
练习册系列答案
相关题目
下列方程是一元一次方程的是（ ）
A、
| ||
B、
| ||
| C、y2+2y=-3 | ||
| D、3x-8y=13 |
如图，已知△ABC，BC=10，BC边的垂直平分线交AB，BC于点E、D．若△ACE的周长为12，则△ABC的周长为下列各式：-
a2b2，
x-1，-25，
，
，π，
，a2-2ab+b2，
中单项式的个数有（ ）
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| x |
| x-y |
| 2 |
| 2a |
| y | ||
|
| A、5个 | B、4个 | C、3个 | D、2个 |
用四舍五入法把2.395精确到百分位后所得的近似数是（ ）
| A、2.39 | B、2.40 |
| C、2.4 | D、2.405 |
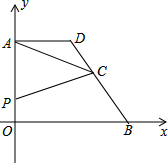如图，直角坐标系中，0是坐标原点，A，B，C三点的坐标分别是A（0，8），B（10，0），C（7，4），AD∥x轴，与直线BC交于点D，动点P从点A出发，以每秒1个单位的速度，沿折线A-O-B的路线移动，移动的时间是t秒，设△ACP的面积是S．
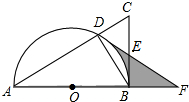如图，AB是⊙O的直径，点D是半圆圆角上的一点，连结AD，过点B作⊙O的切线BC交AD的延长线于点C，E为BC的中点，连结DE，延长DE交AB的延长线于点F，连接BD．