Question

已知⊙O中弦AB⊥弦CD于E，tan∠ACD=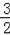

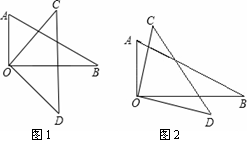
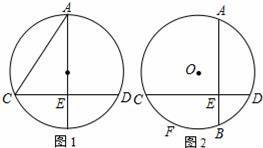
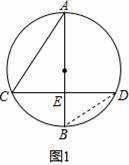
（1）如图1，若AB为⊙O的直径，BE=8，求AC的长

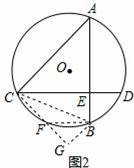
（2）如图2，若AB不为⊙O的直径，BE=4，F为弧BC上一点，弧BF=弧BD，且CF=7，求AC的长．

　

Answer 1

【考点】垂径定理；全等三角形的判定与性质；勾股定理．

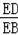
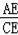
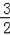
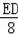
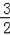
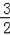
【分析】（1）连接BD，根据垂径定理求得CE=DE，根据圆周角定理得出∠ACD=∠ABD，从而得出==，即=，求得CE=ED=12，根据tan∠ACD=，求得AE=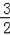CE=18，然后应用勾股定理即可求得AC．

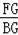
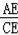
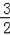
（2）连接CB，过B作BG⊥CF于G，由弧BF=弧BD，得出∠BCE=∠BCG，根据AAS证得△CEB≌△CGB，从而求得BG=BE=4，CE=CG，根据圆内接四边形的性质得出∠BFG=∠A，从而求得△BFG∽△CAE，根据相似三角形对应边成比例得出==，求得FB=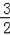BG=6，进而求得CE=CG=13，然后根据勾股定理即可求得AC的长．

【解答】解：（1）如图1，连接BD，

∵直径AB⊥弦CD，

∴CE=DE，

∵∠ACD=∠ABD，

∴tan∠ABD=tan∠ACD=，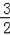

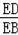
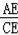
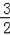
∴==，即=，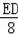

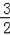
∴ED=12，

∴CE=ED=12，

∴AE=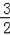CE=18，

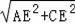
∴AC==6．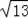

（2）连接CB，过B作BG⊥CF于G，

∵弧BF=弧BD，

∴∠BCE=∠BCG，

在△CEB和△CGB中

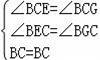
∴△CEB≌△CGB（AAS），

∴BG=BE=4，

∵∠BFG=∠A，∠FGB=∠AEC=90°，

∴△BFG∽△CAE，

∴==，

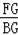
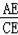
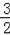
∴FG=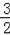BG=6，

∴CE=CG=13，

∴AC=．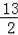

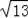
【点评】本题考查了垂径定理、圆周角定理、圆内接四边形的性质、全等三角形的判定和性质，相似三角形的判定和性质、勾股定理的应用，（2）作出辅助线关键全等三角形是解题的关键．