题目内容
1．
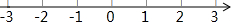解不等式组，并把解集表示在数轴上．$\begin{array}{l}\left\{\begin{array}{l}2x+5≤3（x+2）\\ \frac{3}{2}x-3＜0\end{array}\right.\end{array}$．
分析 分别求出各不等式的解集，再求出其公共解集并在数轴上表示出来即可．
解答 解：$\left\{\begin{array}{l}{2x+5≤3（x+2）①}\\{\frac{3}{2}x-3＜0②}\end{array}\right.$
由①得x≥-1；
由②得x＜2；
∴原不等式组的解集为-1≤x＜2．
在数轴上表示为：
点评 本题考查的是解一元一次不等式组及在数轴上表示不等式组的解集，熟知实心圆点与空心圆点的区别是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
14．若一次函数y=kx的图象经过（3，2），则k的值为（ ）
| A． | -$\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | -$\frac{2}{3}$ | D． | $\frac{2}{3}$ |
15．若m＜1，则（m-1）x＞1-m的解集为（ ）
| A． | x＞1 | B． | x＜1 | C． | x＜-1 | D． | x＞-1 |
11．方程x（x+3）=x+3的根是（ ）
| A． | x=-3 | B． | x1=1，x2=-3 | C． | x1=3，x2=0 | D． | x1=0，x2=3 |
6．在Rt△ABC中，AD是斜边BC上的高，若CB=a，∠B=β，则AD等于（ ）
| A． | asin2β | B． | acos2β | C． | asinβcosβ | D． | asinβtanββ |
已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成，一圆过A、D、E三点，则该圆半径为2．