题目内容
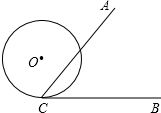
如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是 cm.
【答案】分析:根据题意画图,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F,连接WE,WF,CW,OC,OW,则四边形OWC是矩形;构造直角三角形利用直角三角形中的30°角的三角函数值,可求得点O移动的距离为OW=CF=WF•cot∠WCF=WF•cot30°= .
.
解答: 解:如图,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F;
解:如图,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F;
连接WE,WF,CW,OC,OW,则OW=CF,WF=1,∠WCF= ∠ACB=30°,
∠ACB=30°,
所以点O移动的距离为OW=CF=WF•cot∠WCF=WF•cot30°= .
.
点评:本题利用了切线的性质,矩形的性质,余切的概念,切线长定理求解.
 .
.解答:
 解:如图,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F;
解:如图,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F;连接WE,WF,CW,OC,OW,则OW=CF,WF=1,∠WCF=
 ∠ACB=30°,
∠ACB=30°,所以点O移动的距离为OW=CF=WF•cot∠WCF=WF•cot30°=
 .
.点评:本题利用了切线的性质,矩形的性质,余切的概念,切线长定理求解.

练习册系列答案
相关题目
 如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是( )
如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
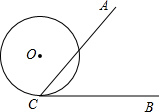 如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( ) 如图,∠ACB=60°,半径为2的⊙0切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为
如图,∠ACB=60°,半径为2的⊙0切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为 如图,∠ACB=60°,⊙O的圆心O在边BC上,⊙O的半径为3,在圆心O向点C运动的过程中,当CO=
如图,∠ACB=60°,⊙O的圆心O在边BC上,⊙O的半径为3,在圆心O向点C运动的过程中,当CO=