题目内容
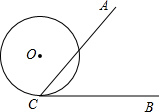 如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )| A、2π | ||
| B、4π | ||
C、2
| ||
| D、4 |
分析:连接O′C,O′B,O′D,OO′,则O′D⊥BC.
因为O′D=O′B,O′C平分∠ACB,可得∠O′CB=
∠ACB=
×60°=30°,由勾股定理得BC=2
.
因为O′D=O′B,O′C平分∠ACB,可得∠O′CB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解答: 解:当滚动到⊙O′与CA也相切时,切点为D,
解:当滚动到⊙O′与CA也相切时,切点为D,
连接O′C,O′B,O′D,OO′,
∵O′D⊥AC,
∴O′D=O′B.
∵O′C平分∠ACB,
∴∠O′CB=
∠ACB=
×60°=30°.
∵O′C=2O′B=2×2=4,
∴BC=
=
=2
.
故选C.
 解:当滚动到⊙O′与CA也相切时,切点为D,
解:当滚动到⊙O′与CA也相切时,切点为D,连接O′C,O′B,O′D,OO′,
∵O′D⊥AC,
∴O′D=O′B.
∵O′C平分∠ACB,
∴∠O′CB=
| 1 |
| 2 |
| 1 |
| 2 |
∵O′C=2O′B=2×2=4,
∴BC=
| O′C2-O′B2 |
| 42-22 |
| 3 |
故选C.
点评:此题主要考查切线及角平分线的性质,勾股定理等知识点,属中等难度题.

练习册系列答案
相关题目
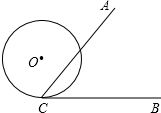 如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是( )
如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
 如图,∠ACB=60°,半径为2的⊙0切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为
如图,∠ACB=60°,半径为2的⊙0切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为 如图,∠ACB=60°,⊙O的圆心O在边BC上,⊙O的半径为3,在圆心O向点C运动的过程中,当CO=
如图,∠ACB=60°,⊙O的圆心O在边BC上,⊙O的半径为3,在圆心O向点C运动的过程中,当CO=