题目内容
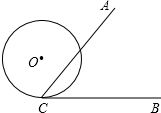如图，∠ACB=60°，半径为1cm的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离是（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
分析：首先作出符合题意的图形，再由切线长定理与切线的性质得到含有30°角的Rt△OCE，利用三角函数即可求得结果．
解答：
解：如图：连接OF，OE，OC，
∵AC与BC都是⊙O的切线，
∴∠1=∠2=
∠ACB=
×60°=30°，OE⊥BC，
∴在Rt△OCE中，tan∠1=tan30°=
=
，
∵OE=1cm，
∴CE=
cm．
故选A．
解：如图：连接OF，OE，OC，∵AC与BC都是⊙O的切线，
∴∠1=∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∴在Rt△OCE中，tan∠1=tan30°=
| OE |
| CE |
| ||
| 3 |
∵OE=1cm，
∴CE=
| 3 |
故选A．
点评：此题考查了切线的性质与切线长定理，以及三角函数等知识．解此题的关键是根据题意作出图形，注意数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
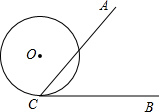如图，∠ACB=60°，半径为2的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为（ ）
如图，∠ACB=60°，半径为2的⊙0切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为
如图，∠ACB=60°，⊙O的圆心O在边BC上，⊙O的半径为3，在圆心O向点C运动的过程中，当CO=