题目内容
 如图,∠ACB=60°,⊙O的圆心O在边BC上,⊙O的半径为3,在圆心O向点C运动的过程中,当CO=
如图,∠ACB=60°,⊙O的圆心O在边BC上,⊙O的半径为3,在圆心O向点C运动的过程中,当CO=2
| 3 |
2
时,⊙O与直线CA相切.| 3 |
分析:过O作OD⊥AC于D,当,⊙O与直线CA相切时,则OD为圆的半径3,进而求出CO的长.
解答: 解:过O作OD⊥AC于D,
解:过O作OD⊥AC于D,
当⊙O与直线CA相切时,则OD为圆的半径3,即OD=3,
∵∠ACB=60°,
∴sin60°=
=
,
∴CO=2
,
故答案为:2
.
 解:过O作OD⊥AC于D,
解:过O作OD⊥AC于D,当⊙O与直线CA相切时,则OD为圆的半径3,即OD=3,
∵∠ACB=60°,
∴sin60°=
| DO |
| CO |
| ||
| 2 |
∴CO=2
| 3 |
故答案为:2
| 3 |
点评:本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为则:直线l和⊙O相切?d=r.

练习册系列答案
相关题目
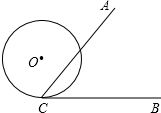 如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是( )
如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
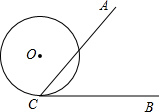 如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( ) 如图,∠ACB=60°,半径为2的⊙0切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为
如图,∠ACB=60°,半径为2的⊙0切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为