题目内容
11. 如图,反比例函数y=$\frac{6}{x}$的图象与一次函数y=kx+b的图象相交于两点A(m,3)和 B(-3,n).
如图,反比例函数y=$\frac{6}{x}$的图象与一次函数y=kx+b的图象相交于两点A(m,3)和 B(-3,n).(1)求一次函数的表达式;
(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量x的取值范围;
(3)求△AOB的面积.
分析 (1)先把A(m,3)和 B(-3,n)分别代入反比例函数解析式求出m、n,于是确定A点坐标为(2,3),B点坐标为(-3,-2),然后利用待定系数法求一次函数的表达式;
(2)根据函数图象,找出反比例函数图象在一次函数图象上方所对应的自变量的范围即可;
(3)设一次函数与x轴交于C点,求出C坐标,确定出OC的长,三角形AOB面积=三角形AOC面积+三角形BOC面积,求出即可.
解答 解:(1)把A(m,3)和 B(-3,n)分别代入y=$\frac{6}{x}$,
得3m=6,-3n=6,
解得m=2,n=-2,
所以A点坐标为(2,3),B点坐标为(-3,-2),
把A(2,3),B(-3,-2)代入y=kx+b,
得$\left\{\begin{array}{l}{2k+b=3}\\{-3k+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
所以这个一次函数的表达式为y=x+1;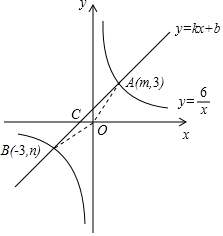 (2)当x<-3或0<x<2时,反比例函数值大于一次函数值;
(2)当x<-3或0<x<2时,反比例函数值大于一次函数值;
(3)连接OA,OB,设一次函数与x轴交于点C,
对于一次函数y=x+1,
令y=0,得到x=-1,
即OC=1,
则S△AOB=S△AOC+S△BOC
=$\frac{1}{2}$×1×3+$\frac{1}{2}$×1×2
=1.5+1
=2.5.
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 △ABC内接于⊙O1,且∠C≥∠B,又⊙O2与⊙O1内切,且与AB、AC边均内切于切点M、N,求证:MN的中点即为△ABC的内心.
△ABC内接于⊙O1,且∠C≥∠B,又⊙O2与⊙O1内切,且与AB、AC边均内切于切点M、N,求证:MN的中点即为△ABC的内心. 如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则点D到直线BC的距离为$\frac{12}{5}$.
如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则点D到直线BC的距离为$\frac{12}{5}$. 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连结AD.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连结AD. 如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,