题目内容
16. 如图所示,已知抛物线y=x2上有一点A.点A的横坐标是-1,过点A作AB∥x轴.交抛物线于另一点B.求△AOB的面积.
如图所示,已知抛物线y=x2上有一点A.点A的横坐标是-1,过点A作AB∥x轴.交抛物线于另一点B.求△AOB的面积.
分析 先求得A点的坐标,进而根据对称性求得B的坐标,从而求得AB=2,然后根据三角形面积公式求得即可.
解答 解:∵抛物线y=x2上有一点A.点A的横坐标是-1,
∴y=1,
∴A(-1,1),
∵B是A的对称点,
∴B(1,1),
∴AB=2,
∴△AOB的面积=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×2×1=1.
点评 本题考查了二次函数图象上点的坐标特征,求得A、B点的坐标是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.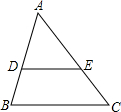 如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )
如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )
 如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )
如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )| A. | 5 | B. | 7 | C. | $\frac{12}{5}$ | D. | 6 |
8.下列各数中,最小的是( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | -3 | D. | -1 |
 如图,在△ABC中,DE垂直平分BC,F为CD中点,求证:EF∥AB.
如图,在△ABC中,DE垂直平分BC,F为CD中点,求证:EF∥AB.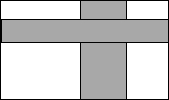 如图,要设计一幅长60cm、宽40cm的图案,其中有一横一竖的彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的$\frac{1}{2}$,求横彩条的宽度.
如图,要设计一幅长60cm、宽40cm的图案,其中有一横一竖的彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的$\frac{1}{2}$,求横彩条的宽度.