题目内容
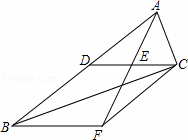
如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
(1)求证:CF=AD;
(2)若∠ACB=90°,试判断四边形BFCD的形状,并说明理由.
(1)证明∵AE是DC边上的中线,
∴AE=FE,
∵CF∥AB,
∴∠ADE=∠CFE,∠DAE=∠CFE.
在△ADE和△FCE中,
 ,
,
∴△ADE≌△FCE(AAS),
∴CF=DA.
(2)∵CD是△ABC的中线,
∴D是AB的中点,
∴AD=BD,
∵△ADE≌△FCE,
∴AD=CF,
∴BD=CF,
∵AB∥CF,
∴BD∥CF,
∴四边形BFCD是平行四边形,
∵∠ACB=90°,
∴△ACB是直角三角形,
∴CD= AB,
AB,
∵BD= AB,
AB,
∴BD=CD,
∴四边形BFCD是菱形.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 b+1 0.
b+1 0.
 切线,切点分别是A、B,如果⊙O的半径为
切线,切点分别是A、B,如果⊙O的半径为 cm,且AB=6cm,求∠ACB.
cm,且AB=6cm,求∠ACB.
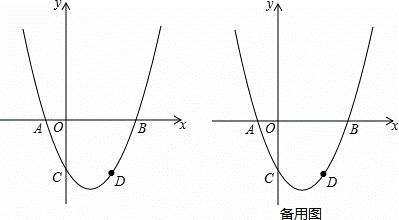
 得到线段CD,则点A的对应点C的坐标为( )
得到线段CD,则点A的对应点C的坐标为( )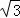 )的抛物线y=
)的抛物线y=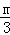 (x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.
(x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C. 使∠BAE=∠BAD,过点D作x轴的垂线交射线AE于点E;
使∠BAE=∠BAD,过点D作x轴的垂线交射线AE于点E;