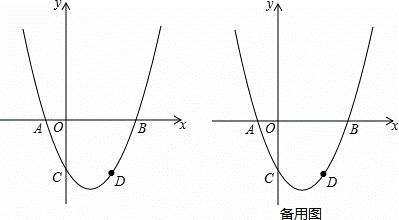
题目内容
如图,已知经过点D(2,﹣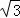 )的抛物线y=
)的抛物线y=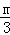 (x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.
(x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.
(1)填空:m的值为 ,点A的坐标为 ;
(2)根据下列描述,用尺规完成作图(保留作图痕迹,不写作法):连接AD,在x轴上方作射线AE, 使∠BAE=∠BAD,过点D作x轴的垂线交射线AE于点E;
使∠BAE=∠BAD,过点D作x轴的垂线交射线AE于点E;
(3)动点M、N分别在射线AB、AE上,求ME+MN的最小值;
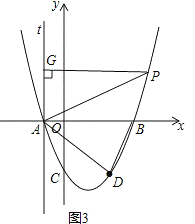
(4)t是过点A平行于y轴的直线,P是抛物线上一点,过点P作l的垂线,垂足为点G,请你探究:是否存在点P,使以P、G、A为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,说明理由.
解:(1)∵抛物线y=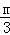 (x+1)(x﹣3)经过点D(2,﹣
(x+1)(x﹣3)经过点D(2,﹣ ),
),
∴m= ,
,
把m= 代入y=
代入y=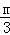 (x+1)(x﹣3),得y=
(x+1)(x﹣3),得y=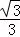 (x+1)(x﹣3),
(x+1)(x﹣3),
即y=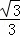 x2﹣
x2﹣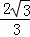 x﹣
x﹣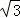 ;
;
令y=0,得(x+1)(x﹣3)=0,
解得x=﹣1或3,
∴A(﹣1,0),B(3,0);
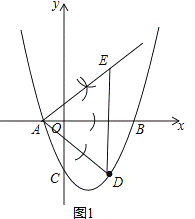
(2)如图1所示;
(3)过点D作射线AE的垂线,垂足为N,交AB于点M,设DE与x轴交于点H,如图2,
由(1)(2)得点D与点E关于x轴对称,
∴MD=ME,
∵AH=3,DH=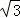 ,
,
∴AD=2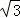 ,
,
∴∠BAD=∠BAE=30°,
∴∠DAN=60°,
∴sin∠DAN=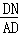 ,
,
∴sin60°=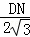 ,
,
∴DN=3,
∵此时DN的长度即为ME+MN的最小值,
∴ME+MN的最小值为3;
(4)假设存在点P,使以P、G、A为顶点的三角形与△ABD相似,如图3,
∵P是抛物线上一点,
∴设点P坐标(x,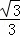 x2﹣
x2﹣ x﹣
x﹣ );
);
∴点G坐标(﹣1,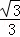 x2﹣
x2﹣ x﹣
x﹣ ),
),
∵A(﹣1,0),B(3,0),D(2,﹣ );
);
∴AB=4,BD=2,AD=2 ,
,
∴△ABD为直角三角形的形状,
△ABD与以P、G、A为顶点的三角形相似,
分两种情况:
①△ABD∽△PAG,
∴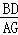 =
=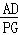 ,
,
∴2(x+1)=2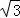 (
(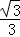 x2﹣
x2﹣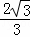 x﹣
x﹣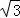 ),
),
解得x1=4,x2=﹣1(舍去),
∴P(4,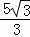 );
);
②△ABD∽△APG,
∴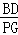 =
=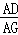 ,
,
∴2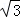 (x+1)=2(
(x+1)=2(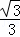 x2﹣
x2﹣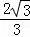 x﹣
x﹣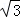 ),
),
解得x1=6,x2=﹣1(舍去),
∴P(6,7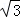 );
);
∴点P坐标(4,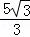 )或(6,7
)或(6,7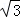 ).
).


 科学实验活动册系列答案
科学实验活动册系列答案 的解在数轴上表示为( )
的解在数轴上表示为( ) B.
B.  C.
C.  D.
D. 

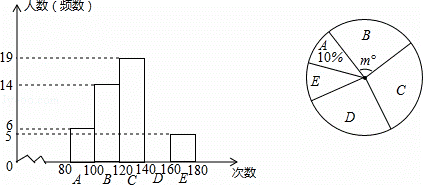
 =90次),则这次调查的样本平均数是多少?
=90次),则这次调查的样本平均数是多少? 3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.