题目内容
求经过点A（0，2）、B（2，0）、C（-1，2）的抛物线的解析式，并求出其最大或最小值．
【答案】分析：根据题意首先设函数解析式为y=ax2+bx+c，把点坐标分别代入解析式即可求出系数，再由配方法求得最大或最小值即可．
解答：解：由题意设二次函数解析式为：y=ax2+bx+c，
把A（0，2）、B（2，0）、C（-1，2）分别代入二次函数解析式，
得：
解得
所以函数解析式为：y=-
x2-
x+2，
配方得：y=-
（x-
）2+
，
所以二次函数有最大值且最大值为：
点评：本题考查的是待定系数法确定函数解析式，是基础题型也是常考题型．
解答：解：由题意设二次函数解析式为：y=ax2+bx+c，
把A（0，2）、B（2，0）、C（-1，2）分别代入二次函数解析式，
得：
解得
所以函数解析式为：y=-
x2-x+2，配方得：y=-
（x-）2+，所以二次函数有最大值且最大值为：
点评：本题考查的是待定系数法确定函数解析式，是基础题型也是常考题型．
练习册系列答案
阅读快车系列答案
相关题目
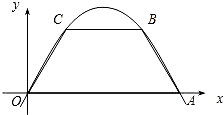如图，在等腰梯形OABC中，CB∥OA，∠COA=60°BC=2，OA=4，且与x轴重合．
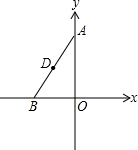如图，在△ABO中，已知A（0，4），B（-2，0），D为线段AB的中点．
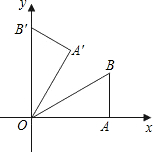绕点O按逆时针方向旋转至△OA′B′，使点B的对应点B′落在y轴的正半轴上，已知OB=2，∠BOA=30°．
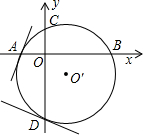为