题目内容
解方程:
(1)x2-5x-6=0;
(2)2x2-4x-1=0;
(3)(x-7)2+2(x-7)=0;
(4)(3x+2)2=4(x-3)2.
(1)x2-5x-6=0;
(2)2x2-4x-1=0;
(3)(x-7)2+2(x-7)=0;
(4)(3x+2)2=4(x-3)2.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)利用因式分解法解方程;
(2)利用配方法解方程;
(3)利用因式分解法解方程;
(4)先两边开方得到3x+2=±2(x-3),然后解两个一元一次方程即可.
(2)利用配方法解方程;
(3)利用因式分解法解方程;
(4)先两边开方得到3x+2=±2(x-3),然后解两个一元一次方程即可.
解答:解:(1)(x-6)(x+1)=0,
x-6=0或x+1=0,
所以x1=6,x2=-1;
(2)x2-2x=
,
x2-2x+1=
+1,
(x-1)2=
x-1=±
,
所以x1=1+
,x2=1-
;
(3)(x-7)(x-7+2)=0,
x-7=0或x-7+2=0,
所以x1=7,x2=5;
(4)3x+2=±2(x-3),
所以x1=-8,x2=
.
x-6=0或x+1=0,
所以x1=6,x2=-1;
(2)x2-2x=
| 1 |
| 2 |
x2-2x+1=
| 1 |
| 2 |
(x-1)2=
| 3 |
| 2 |
x-1=±
| ||
| 2 |
所以x1=1+
| ||
| 2 |
| ||
| 2 |
(3)(x-7)(x-7+2)=0,
x-7=0或x-7+2=0,
所以x1=7,x2=5;
(4)3x+2=±2(x-3),
所以x1=-8,x2=
| 4 |
| 5 |
点评:本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了用配方法解一元二次方程.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
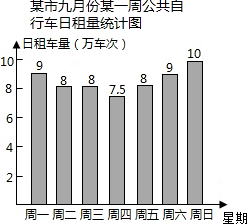 作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对2014年九月份中的7天进行了公共自行车日租车量的统计,结果如图:
作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对2014年九月份中的7天进行了公共自行车日租车量的统计,结果如图: