Question

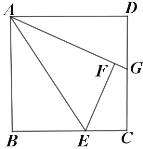
【题目】如图，已知正方形的边长为6，点是上的点，，将沿着直线翻折，点落在点处，的延长线交线段于，则的长度是____．

Answer 1

【答案】

【解析】

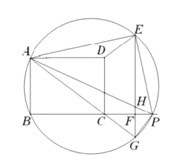
延长AE与DC的延长线交于H，根据翻折变换的性质可得AF＝AB，∠BAE＝∠FAE，再根据两直线平行，内错角相等可得∠BAE＝∠H，从而得到∠GAE＝∠H，根据等角对等边可得AG＝GH，设CG＝x，表示出DG、AG，然后利用勾股定理列方程求出x的值，从而得到CG的值．

解：延长AE与DC的延长线交于H，

∵△ABE沿直线AE翻折，点B落在点F处，

∴AF＝AB＝6，∠BAE＝∠FAE，
∵正方形对边AB∥CD，
∴∠BAE＝∠H，
∴∠GAE＝∠H，
∴AG＝HG，

∵正方形ABCD，

∴∠B=∠BCH=90°，

∵∠AEB=∠HEC

∴△AEB∽△HEC

∴

∵，
∴CH＝3，
设CG＝x，

∴DG＝6x，AG＝HG＝3＋x，
在Rt△ADG中，由勾股定理得，AG2＝AD2＋DG2，
即（3＋x）2＝62＋（6x）2，
解得x＝

∴CG=

故答案为：