Question

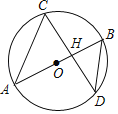
【题目】如图，AB是⊙O的直径，且经过弦CD的中点H，已知sin∠CDB=，BD=5，则AH的长为（　　）

A. B. C. D.

Answer 1

【答案】B

【解析】连接OD，由垂径定理得出AB⊥CD，由三角函数求出BH=3，由勾股定理得出DH==4，设OH=x，则OD=OB=x+3，在Rt△ODH中，由勾股定理得出方程，解方程即可．

连接OD，如图所示：

∵AB是⊙O的直径，且经过弦CD的中点H，

∴AB⊥CD，

∴∠OHD=∠BHD=90°，

∵sin∠CDB=，BD=5，

∴BH=3，

∴DH==4，

设OH=x，则OD=OB=x+3，

在Rt△ODH中，由勾股定理得：x2+42=（x+3）2，

解得：x=，

∴OH=，

∴AH=OA+OH=+3+=，

故选B．