题目内容
7.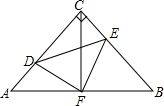 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在边AC、BC边上,且AD=CE,连接DE、DF、EF.
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在边AC、BC边上,且AD=CE,连接DE、DF、EF.(1)求证:△ADF≌△CEF;
(2)试判断△DFE的形状,并说明理由.
分析 (1)根据F是AB中点,可得AF=BF=CF,∠A=∠FCE=45°,即可证明△ADF≌△CEF;
(2)根据△ADF≌△CEF可得DF=EF,∠AFD=∠CFE,即可求得∠DFE=90°,即可解题.
解答 (1)证明:∵F是AB中点,AC=BC,∠ACB=90°,
∴AF=BF=CF,∠A=∠FCE=45°,
在△ADF和△CEF中,
$\left\{\begin{array}{l}{AF=CF}\\{∠A=∠FCE=45°}\\{AD=CE}\end{array}\right.$,
∴△ADF≌△CEF(SAS);
(2)解:△DEF是等腰直角三角形.理由如下:
∵△ADF≌△CEF,
∴DF=EF,∠AFD=∠CFE,
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFE=90°,即∠DFE=90°,
∴△DEF是等腰直角三角形.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,本题中求证△ADF≌△CEF是解题的关键.

练习册系列答案
相关题目
12.某校九年级(2)班积极响应学校的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书320册.特别值得表扬的是李亮和王州两位同学,他们各捐献了50册图书.班长统计了全班捐书情况如表,被粗心的马小虎用墨水污染了一部分:
(1)分别求出该班级捐献7册图书和8册图书的人数.
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪些统计量不能反映该班同学捐书册数的一般状况,说明理由.
| 册数 | 4 | 5 | 6 | 7 | 8 | 50 |
| 人数 | 6 | 8 | 15 | 2 |
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪些统计量不能反映该班同学捐书册数的一般状况,说明理由.

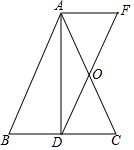 如图,已知在△ABC中,D为BC上一点,连接AD,过点A作AF∥BC,过点D作DF∥AB,AF与DF交于点F,DF与AC交于点O,若AO=OC.
如图,已知在△ABC中,D为BC上一点,连接AD,过点A作AF∥BC,过点D作DF∥AB,AF与DF交于点F,DF与AC交于点O,若AO=OC. 已知:a∥b,∠3=137°,则∠1=137°,∠2=43°.
已知:a∥b,∠3=137°,则∠1=137°,∠2=43°.