题目内容
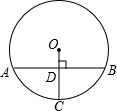 如图,在⊙O中,半径OC垂直弦AB于点D,交⊙O于点C,若OD=2,AB=8
如图,在⊙O中,半径OC垂直弦AB于点D,交⊙O于点C,若OD=2,AB=8| 2 |
| A、6 | B、5 | C、4 | D、3 |
考点:垂径定理,勾股定理
专题:
分析:连接OA,先根据垂径定理得出AD的长,再由勾股定理求出OA的长,进而可得出结论.
解答: 解:连接OA,
解:连接OA,
∵OC⊥AB,AB=8
,
∴AD=
AB=4
.
在Rt△AOD中,
OA=
=
=6,
∴OC=OA=6,
∴CD=OC-OD=6-2=4.
故选C.
 解:连接OA,
解:连接OA,∵OC⊥AB,AB=8
| 2 |
∴AD=
| 1 |
| 2 |
| 2 |
在Rt△AOD中,
OA=
| OD2+AD2 |
22+(4
|
∴OC=OA=6,
∴CD=OC-OD=6-2=4.
故选C.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、倒数等于它本身的数是1 |
| B、0是绝对值最小的数 |
| C、平方等于它本身的数是0 |
| D、-1是最大的负数 |
用配方法解方程x2-5x=4,应把方程的两边同时( )
A、加上
| ||
B、加上
| ||
C、减去
| ||
D、减去
|





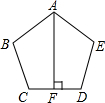 已知,如图,AB=AE,∠BAF=∠EAF,AF⊥CD,且F为CD中点,试说明:BC=ED.
已知,如图,AB=AE,∠BAF=∠EAF,AF⊥CD,且F为CD中点,试说明:BC=ED.