题目内容
等腰三角形ABC的底边BC=6,△ABC的外接圆⊙O的半径为5,则S△ABC= .
考点:垂径定理,等腰三角形的性质,勾股定理
专题:
分析:根据等腰三角形的性质,以及垂径定理的性质,作出三角形的高,即可求出,应注意底边BC与圆心可能存在两种位置关系可能.
解答: 解:连接AO,并延长与BC交于一点D,连接OC,
解:连接AO,并延长与BC交于一点D,连接OC,
∵BC=6cm,⊙O的半径为5cm,AB=AC,
∴AD⊥BC,
∴OD=4,AD=9,
∴△ABC的面积为27,
同理当BC在圆心O的上方时,三角形的高变为5-4=3,
∴△ABC的面积为8.
故答案为:8或27.
 解:连接AO,并延长与BC交于一点D,连接OC,
解:连接AO,并延长与BC交于一点D,连接OC,∵BC=6cm,⊙O的半径为5cm,AB=AC,
∴AD⊥BC,
∴OD=4,AD=9,
∴△ABC的面积为27,
同理当BC在圆心O的上方时,三角形的高变为5-4=3,
∴△ABC的面积为8.
故答案为:8或27.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,数轴的画法正确的是( )
A、 |
B、 |
C、 |
D、 |
数轴上A、B两点分别表示-4
和3,那么A、B两点的距离是( )
| 1 |
| 2 |
A、-1
| ||
B、7
| ||
C、1
| ||
D、-
|
下列式子能成立的是( )
| A、(a-b)2=a2-ab+b2 |
| B、(a+3b)2=a2+9b2 |
| C、(a+b)2=a2+2ab+b2 |
| D、(x+3)(x-3)=x2-x-9 |
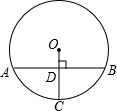 如图,在⊙O中,半径OC垂直弦AB于点D,交⊙O于点C,若OD=2,AB=8
如图,在⊙O中,半径OC垂直弦AB于点D,交⊙O于点C,若OD=2,AB=8| 2 |
| A、6 | B、5 | C、4 | D、3 |
已知实数x,y满足|x-3|+
=0,则代数式(x+y)2014的值为( )
| y+4 |
| A、-1 | B、1 |
| C、2014 | D、-2008 |
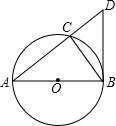 如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D. Rt△ABC中,∠C=90°,∠ABC=30°,点A(0,1),点B、点C在反比例函数y=
Rt△ABC中,∠C=90°,∠ABC=30°,点A(0,1),点B、点C在反比例函数y=