题目内容
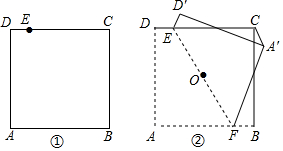
14.在正方形ABCD中,AB=8,E、F分别为DC、AB上一点,将正方形ABCD沿EF折叠,点A、D分别落在点A′、D′的位置.(1)若点A′恰好落在BC上.①在图①中,利用直尺和圆规确定点F的位置(保留作图痕迹,不写作法);
②连接AA′,已知DE=1,求AA′的长度.
(2)如图②,EF经过正方形ABCD的对称中心O,连接A′C,若DE=1,则A′C的长度是$\frac{8}{5}$.
分析 (1)①如图①中,a、以E为圆心.,EA为半径画弧交BC于A′,连接EA、EA′.b、作∠AEA′的平分线EK交AB于F.点F即为所求;
②分别求出AE、A′E、CA′、A′B,在Rt△ABA′中利用勾股定理即可解决问题;
(2)如图②中,连接AC、BD与EF交于点O,作EM⊥BD于M′,连接OA′,AA′交EF于N.求出Rt△EMO的三边,由△AA′C∽△OME,可得$\frac{A′C}{EM}$=$\frac{AC}{OE}$,即可解决问题;
解答 解:(1)①如图①中,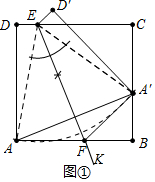
a、以E为圆心.,EA为半径画弧交BC于A′,连接EA、EA′.
b、作∠AEA′的平分线EK交AB于F.
点F即为所求.
②∵四边形ABCD是正方形,
∴AD=AB=BC=CD=8,∠D=∠C=∠B=90°,
在Rt△ADE中,AE2=AD2+DE2=64+1=65,
在Rt△ECA′中,A′C=$\sqrt{65-49}$=4,
∴A′B=BC-A′C=4,
在Rt△ABA′中,AA′=$\sqrt{A{B}^{2}+BA{′}^{2}}$=$\sqrt{64+16}$=4$\sqrt{5}$.
(2)如图②中,连接AC、BD与EF交于点O,作EM⊥BD于M′,连接OA′,AA′交EF于N.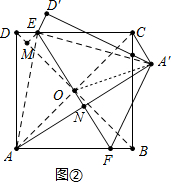
易知DM=EM=$\frac{\sqrt{2}}{2}$,OD=4$\sqrt{2}$,
∴OM=$\frac{7\sqrt{2}}{2}$,
在Rt△OME中,OE=$\sqrt{O{M}^{2}+E{M}^{2}}$=$\sqrt{(\frac{7\sqrt{2}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=5,
∵OA=OA′=OC,
∴∠AA′C=90°,
∵∠DOA=90°,
∴∠EOM+∠AON=90°,
∵∠OAN+∠AON=90°,
∴∠EOM=∠CAA′,∵∠AA′C=∠OME,
∴△AA′C∽△OME,
∴$\frac{A′C}{EM}$=$\frac{AC}{OE}$,
∴$\frac{A′C}{\frac{\sqrt{2}}{2}}$=$\frac{8\sqrt{2}}{5}$,
∴CA′=$\frac{8}{5}$.
故答案为$\frac{8}{5}$.
点评 本题考查正方形的性质、翻折变换、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案方案一:在多家旅游公司调查400名导游;
方案二:在野鸭湖国家湿地公园调查400名游客;
方案三:在玉渡山风景区调查400名游客;
方案四:在上述四个景区各调查100名游客.
在这四个收集数据的方案中,最合理的是( )
| A. | 方案一 | B. | 方案二 | C. | 方案三 | D. | 方案四 |
| A. | 直径 | B. | 周长 | C. | 面积 | D. | 半径 |
| A. | -$\frac{2}{5}$,2 | B. | $\frac{2}{5}$,3 | C. | -$\frac{2}{5}$,5 | D. | $\frac{2}{5}$,6 |
 在平面直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B.
在平面直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B.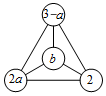 如图,在一个三角形三个顶点和中心处的每个“○”中各填有一个式子,如果图中任意三个“○”中的式子之和均相等,那么a的值为( )
如图,在一个三角形三个顶点和中心处的每个“○”中各填有一个式子,如果图中任意三个“○”中的式子之和均相等,那么a的值为( )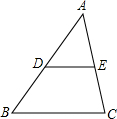 如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.
如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.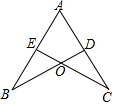 如图,已知∠B=∠C,要判断△ABD≌△ACE,若根据“ASA”,还需要的条件是AB=AC若根据“AAS”,则还需要的条件是BD=CE或AD=AE.
如图,已知∠B=∠C,要判断△ABD≌△ACE,若根据“ASA”,还需要的条件是AB=AC若根据“AAS”,则还需要的条件是BD=CE或AD=AE.