题目内容
如图,在平面直角坐标系xO y中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
y中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
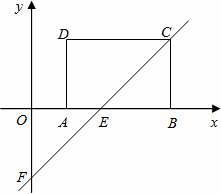 (1)求矩形ABCD的顶点A、B、C、D的坐标;
(1)求矩形ABCD的顶点A、B、C、D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x-2上一点,若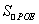 =5,求点P的坐标.
=5,求点P的坐标.
(1)点A、B、C、D的坐标分别为(1,0)、(4,0)、(4,2),(1,2).
(2)(2)直线y=x-2与x轴、y轴坐标分别为E (2,0)、F (0,-2),
∴OF=OE=BC=BE=2,在RT△OEF和RT△BEC中,
 ,故可得△
,故可得△ OEF≌△BEC.
OEF≌△BEC.
(3)设点P的坐标为 ,则
,则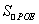 =
= ×OE×
×OE× =
= ×2×
×2× =5,
=5,
解得: =±5,
=±5,
①当 =5时,
=5时, =7;②当
=7;②当 =-5时,
=-5时, =-3,
=-3,
故点P的坐标为(7,5)或(-3,-5).

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目

 00元.
00元. ,求y与x之间的函数关系式;
,求y与x之间的函数关系式; (3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种 方案能使获利最大?最大获利为多少元?
方案能使获利最大?最大获利为多少元? 已知直线
已知直线 与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),则
与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),则 的取值范围是 .
的取值范围是 . 和
和 ,
, 的立方根是-2,求
的立方根是-2,求 的算术平方根.
的算术平方根. ,4.11212121212…,0,
,4.11212121212…,0, 中,无理数有( )
中,无理数有( )

 ,则a的取值范围是( )
,则a的取值范围是( )