Question

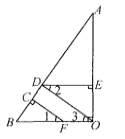
【题目】如图，在△ABC中，∠BAC＝30°，以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点，且BC=CD ，弦AD的延长线交切线PC于点E，连接BC．

（1）判断OB和BP的数量关系,并说明理由；

（2）若⊙O的半径为2，求AE的长．

Answer 1

【答案】（1）OB=BP，理由见解析（2）3

【解析】

（1）由题文过C点切线，可连接OC得垂直，又根据直角三角形中30°所对的直角边等于斜边的一半，可得OB=BP.

（2）由（1）可知AP的长，且∠P=30°，若∠E=90°，则可得AE=AP=3.又已知BC=CD,则∠BAD=60°，所以在△APE中∠E=90°.继而得到答案.

解：（1）OB=BP.

连接OC，

∵PC切⊙O于点C，∴∠OCP=90°.

∵OA=OC，∠OAC=30°，∴∠OAC=∠OCA=30°.

∴∠COP=60°.∴∠P=30°.

在Rt△OCP中，OB=OC=OP= BP.

（2）由（1）得OB=OP.

∵⊙O的半径是2，∴AP=3OB=3×2=6.

又∵BC=CD，∴∠CAD=∠BAC=30°，∠BAD=60°.

∵∠P=30°，∴∠E=90°.

在Rt△AEP中，AE=AP=×6=3.