ЬтФПФкШн
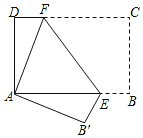
ЁОЬтФПЁП(1)ШчЭМ1,дкЫФБпаЮABCDжаЃЌAB=ADЃЌЁЯBAD=120ЁуЃЌЁЯB=ЁЯADC=90ЁуЃЌEЁЂFЗжБ№ЪЧBCЁЂCDЩЯЕФЕуЃЎЧвBE+DF=EFЃЎЪдЧѓЁЯEAFЖШЪ§ЃЎ
аЁЭѕЭЌбЇЬНОПДЫЮЪЬтЕФЗНЗЈЪЧЃЌбгГЄFDЕНЕуGЃЎЪЙDG=BEЃЎСЌНсAGЃЌЯШжЄУїЁїABEЁеЁїADGЃЌдйжЄУїЁїAEFЁеЁїAGFЃЌПЩЕУЧѓГіЁЯEAFЖШЪ§ЃЌЫћЧѓГіЕФЁЯEAFЖШЪ§гІЪЧ ЃЎЧыФуИљОнЫћЕФЫМТЗЭъГЩТлжЄЙ§ГЬ.
(2)ШчЭМ2ЃЌШєдкЫФБпаЮABCDжаЃЌAB=ADЃЌЁЯB+ЁЯD=180ЁуЃЎEЃЌFЗжБ№ЪЧBCЃЌCDЩЯЕФЕуЃЌЪдЬНОПЕБЁЯEAFгыЁЯBADТњзуЪВУДЙиЯЕЪБгаBE+DF=EFЃЌВЂЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ60ЁуЃЛЃЈ2ЃЉЕБЁЯEAFЃН![]() ЁЯBADЪБгаBE+DF=EFЃЌРэгЩМћНтЮі.
ЁЯBADЪБгаBE+DF=EFЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄFDЕНЕуGЃЎЪЙDGЃНBEЃЎСЌНсAGЃЌМДПЩжЄУїЁїABEЁеЁїADGЃЌПЩЕУAEЃНAGЃЌдйжЄУїЁїAEFЁеЁїAGFЃЌПЩЕУЁЯEAFЃНЁЯGAFЃЌМДПЩНтЬтЃЛ
ЃЈ2ЃЉбгГЄFDЕНЕуGЃЎЪЙDGЃНBEЃЎСЌНсAGЃЌМДПЩжЄУїЁїABEЁеЁїADGЃЌПЩЕУAEЃНAGЃЌдйжЄУїЁїAEFЁеЁїAGFЃЌПЩЕУЁЯEAFЃНЁЯGAFЃЌМДПЩНтЬтЃЎ
НтЃКЃЈ1ЃЉдкЁїABEКЭЁїADGжаЃЌ ЃЌ
ЃЌ
ЁрЁїABEЁеЁїADGЃЈSASЃЉЃЌ
ЁрAEЃНAGЃЌЁЯBAEЃНЁЯDAGЃЌ
ЁпBE+DF=EFЃЌ
ЁрDG+DF=EFЃЌМДGF=EFЃЌ
дкЁїAEFКЭЁїAGFжаЃЌ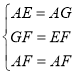 ЃЌ
ЃЌ
ЁрЁїAEFЁеЁїAGFЃЈSSSЃЉЃЌ
ЁрЁЯEAFЃНЁЯGAFЃЌ
ЁрЁЯEAFЃНЁЯFAD+ЁЯDAGЃЌМДЁЯEAFЃНЁЯFAD+ЁЯBAEЃЌ
ЁрЁЯEAFЃН![]() ЁЯBADЃН60ЁуЃЛ
ЁЯBADЃН60ЁуЃЛ
ЃЈ2ЃЉЕБЁЯEAFЃН![]() ЁЯBADЪБгаBE+DF=EFЃЌ
ЁЯBADЪБгаBE+DF=EFЃЌ
РэгЩЃКбгГЄFDЕНЕуGЃЌЪЙDGЃНBEЃЎСЌНсAGЃЌ
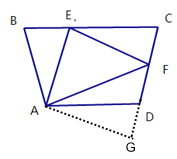
ЁпЁЯB+ЁЯADF=180ЁуЃЌЁЯADF+ЁЯADG=180ЁуЃЌ
ЁрЁЯB=ЁЯADGЃЌ
дкЁїABEКЭЁїADGжаЃЌ ЃЌ
ЃЌ
ЁрЁїABEЁеЁїADGЃЈSASЃЉЃЌ
ЁрAEЃНAGЃЌЁЯBAEЃНЁЯDAGЃЌ
ЁпBE+DF=EFЃЌ
ЁрDG+DF=EFЃЌМДGF=EFЃЌ
дкЁїAEFКЭЁїAGFжаЃЌ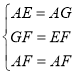 ЃЌ
ЃЌ
ЁрЁїAEFЁеЁїAGFЃЈSSSЃЉЃЌ
ЁрЁЯEAFЃНЁЯGAFЃЌ
ЁрЁЯEAFЃНЁЯFAD+ЁЯDAGЃЌМДЁЯEAFЃНЁЯFAD+ЁЯBAEЃЌ
ЁрЁЯEAFЃН![]() ЁЯBADЃЌ
ЁЯBADЃЌ
ЁрЕБЁЯEAFЃН![]() ЁЯBADЪБгаBE+DF=EF.
ЁЯBADЪБгаBE+DF=EF.

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ