Question

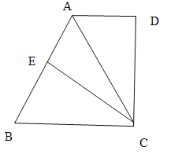
【题目】如图，在梯形ABCD中，∠BCD=∠D=90，上底AD=3，下底BC=，高CD=4，沿AC把梯形ABCD翻折，点D是恰好落在AB边上的点E处，求△BCE面积。

Answer 1

【答案】 .

【解析】

先根据梯形的面积计算公式求出梯形的面积，再根据三角形的面积计算公式求出三角形ACD的面积，然后根据折叠的性质，可得到三角形ACE的面积，三角形BCE的面积=梯形的面积-三角形ACD的面积-三角形ACE的面积，从而问题得解.

解：∵△ACE是△ACD折叠得到，

∴∠AEC=∠D=90°，AE=AD=3,CE=CD=4.

∴△ACE的面积=△ACD的面积=43=6.

∵梯形ABCD的面积=

∴△BCE面积=梯形ABCD的面积-△ACE的面积-△ACD的面积

= -6-6

=

答：△BCE面积是 .