题目内容
把二次函数y=x2-2x+3配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,y<0时x的取值范围,并画出图象.
考点:二次函数的三种形式
专题:计算题
分析:利用配方法得到y=(x-1)2+2,则可确定抛物线的顶点坐标、对称轴方程,然后利用描点法画出抛物线,由图象可得x无论取何值,y>0.
解答:解:y=x2-2x+3=(x-1)2+2,则抛物线的顶点坐标为(1,2),对称轴为直线x=1;x无论取何值,y>0.
如图:

如图:

点评:本题考查了二次函数的解析式的三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
相关题目
 已知a,b,c表示的数如图所示,则-a,-b,-c由小到大的顺序是( )
已知a,b,c表示的数如图所示,则-a,-b,-c由小到大的顺序是( )| A、-a<-b<-c |
| B、-c<-a<-b |
| C、-a<-c<-b |
| D、-b<-c<-a |
 如图,已知l1∥l2∥l3,AC,DF交于点O,且
如图,已知l1∥l2∥l3,AC,DF交于点O,且 如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=70°,则∠α=
如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=70°,则∠α= 如图,已知:∠BME=∠CPF,直线EF分别交AB、CD于M、P,MN、PQ分别平分∠AME、∠DPF,求证:
如图,已知:∠BME=∠CPF,直线EF分别交AB、CD于M、P,MN、PQ分别平分∠AME、∠DPF,求证:
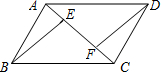 如图,四边形ABCD是平行四边形,点E、F在对角线AC上,连接BE、DF.∠ABE=∠CDF.求证:△ADF≌△CBE.
如图,四边形ABCD是平行四边形,点E、F在对角线AC上,连接BE、DF.∠ABE=∠CDF.求证:△ADF≌△CBE. ,则实际纸上的号码是
,则实际纸上的号码是