题目内容
7.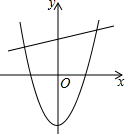 已知抛物线y=x2+h与x轴交于A、B两点,与y轴交于C点,且OC=AB.
已知抛物线y=x2+h与x轴交于A、B两点,与y轴交于C点,且OC=AB.(1)求此抛物线的解析式;
(2)直线y=2x+b被抛物线截得线段长为2$\sqrt{30}$,求b.
分析 (1)由题意设点B坐标(-$\frac{1}{2}$h,0),把点B坐标代入y=x2+h得到0=$\frac{1}{4}$h2+h,解方程即可解决问题.
(2)设直线y=2x+b与抛物线y=x2-4的交点为E(x1,y1),F(x2,y2),由$\left\{\begin{array}{l}{y={x}^{2}-4}\\{y=2x+b}\end{array}\right.$消去y得到x2-2x-4-b=0,可得x1+x2=2,x1x2=-4-b,由此推出y1+y2=4+2b,y1y2=b2-16,所以(x1-x2)2=(x1+x2)2-4x1x2=4b+20,同理可得(y1-y2)2=16b+80,根据EF=2$\sqrt{30}$,列出方程即可解决问题.
解答 解:(1)如图由题意,OA=OB,
∵OC=AB,
∴OA=OB=-$\frac{1}{2}$h,
∴点B坐标(-$\frac{1}{2}$h,0),
把点B坐标代入y=x2+h得到,0=$\frac{1}{4}$h2+h,解得h=-4或0(舍弃),
∴抛物线的解析式为y=x2-4.
(2)设直线y=2x+b与抛物线y=x2-4的交点为E(x1,y1),F(x2,y2).
由$\left\{\begin{array}{l}{y={x}^{2}-4}\\{y=2x+b}\end{array}\right.$消去y得到x2-2x-4-b=0,
∴x1+x2=2,x1x2=-4-b,由此可得y1+y2=4+2b,y1y2=b2-16,
∴(x1-x2)2=(x1+x2)2-4x1x2=4b+20,同理可得(y1-y2)2=16b+80,
∵EF=2$\sqrt{30}$,
∴4b+20+16b+80=120,
∴b=1.
点评 本题考查抛物线与x轴的交点、一次函数、待定系数法、两点之间距离公式等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,把问题转化为方程组,利用根与系数关系解决问题,属于中考常考题型.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案| A. | 3600(1+x)2=6000 | B. | 6000(1+x)2=3600 | C. | 6000(x-1)2=3600 | D. | 6000(1-x)2=3600 |
| A. | -5 | B. | 0 | C. | 52002 | D. | 4×52003 |
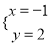 是二元一次方程组
是二元一次方程组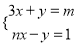 的
的 解,则m-n的值是( )
解,则m-n的值是( )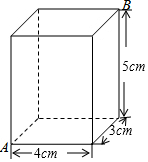 图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少? 将下列实数与它们在数轴上的对应点连起来,并把这些数按从小到大的顺序排列,用“<”连接
将下列实数与它们在数轴上的对应点连起来,并把这些数按从小到大的顺序排列,用“<”连接 如图,数轴上A、B所对应的数分别为-5、10,O为原点,点P以每秒2个单位长度,点Q以每秒3个单位长度,分别自A、B两点同时出发,在数轴上运动,设运动时间为t秒,若点P、Q相向而行且OP=OQ,求t值.
如图,数轴上A、B所对应的数分别为-5、10,O为原点,点P以每秒2个单位长度,点Q以每秒3个单位长度,分别自A、B两点同时出发,在数轴上运动,设运动时间为t秒,若点P、Q相向而行且OP=OQ,求t值. = _____________
= _____________