题目内容
10．
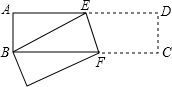已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与D重合，折痕为EF，则BE的长为（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | 6cm |
分析 根据折叠的性质可得BE=ED，设AE=x，表示出BE=9-x，然后在Rt△ABE中，利用勾股定理列式计算即可得解．
解答 解：∵长方形折叠点B与点D重合，
∴BE=ED，
设AE=x，则ED=9-x，BE=9-x，
在Rt△ABE中，AB2+AE2=BE2，
即32+x2=（9-x）2，
解得x=4，
∴AE的长是4，
∴BE=9-4=5，
故选C．
点评 本题考查了翻折变换的性质，勾股定理的应用，根据勾股定理列出关于AE的长的方程是解题的关键．
练习册系列答案
相关题目
1．下面的数中，与-2的和为0的是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
19．如图，下列图案均是长度相同的火柴按一定的规律拼搭而成，每个围成的正方形面积为1cm2：第1个图案面积为2cm2，第2个图案面积为4cm2，第3个图案面积为7cm2…，依此规律，第8个图案面积为（ ）cm2．
| A． | 35 | B． | 36 | C． | 37 | D． | 38 |
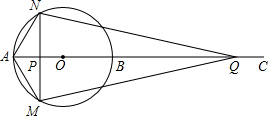如图，AB为⊙O的直径，点C为AB延长线上一点，动点P从点A出发沿AC方向以lcm/s的速度运动，同时动点Q从点C出发以相同的速度沿CA方向运动，当两点相遇时停止运动，过点P作AB的垂线，分别交⊙O于点M和点N，已知⊙O的半径为l，设运动时间为t秒．
14．下列运算正确的是（ ）
| A． | x2+x3=x6 | B． | （x3）2=x6 | C． | 2x+3y=5xy | D． | x6÷x3=x2 |
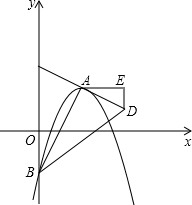如图，在平面直角坐标系xOy中，抛物线y=-$\frac{1}{4}$（x-m）2+$\frac{1}{4}$m2-m的顶点为A，与y轴的交点为B，连结AB，AC⊥AB，交y轴于点C，延长CA到点D，使AD=AC，连结BD．作AE∥x轴，DE∥y轴．
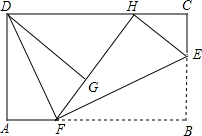如图，已知长方形的每个角都是直角，将长方形ABCD沿EF折叠后点B