题目内容
18.若y=$\frac{{\sqrt{{x^2}-4}+\sqrt{4-{x^2}}}}{x+2}$-1,化简求值[(2x+y)2-y(x+y)-4xy]÷2x.分析 根据二次根式有意义的条件:被开方数是非负数即可求得x的值,则y的值即可求得.首先利用完全平方公式和单项式与多项式的乘法法则计算,对括号内的式子合并同类项,然后计算除法即可化简,最后代入数值计算即可.
解答 解:根据题意得:x2-4=0,解得x=2或-2.
又∵x+2≠0,即x≠-2.
∴x=2.
则y=-1.
原式=(4x2+4xy+y2-xy-y2-4xy)÷2x
=(4x2-xy)÷2x
=2x-$\frac{1}{2}$y,
当x=2,y=-1时,原式=4+$\frac{1}{2}$=$\frac{9}{2}$.
点评 本题考查了二次根式有意义的条件以及整式的化简求值,正确理解完全平方公式以及二次根式的性质求得x的值是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列各式中,正确的是( )
| A. | x2-2x2=-x2 | B. | 2a+3b=5ab | C. | 7ab-3ab=4 | D. | a3+a2=a5 |
10.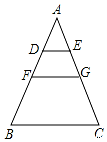 如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
 如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )| A. | 1:8:27 | B. | 1:4:9 | C. | 1:8:36 | D. | 1:9:36 |