题目内容
20．
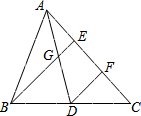如图，已知AD是△ABC的中线，AE=EF=FC，下面给出三个关系式：①AD=2AG；②GE：BE=1：3；③$\frac{{{S_{△CDF}}}}{{{S_{△BDG}}}}=\frac{2}{3}$，
其中正确的是（ ）
| A． | ①② | B． | ①②③ | C． | ①③ | D． | ②③ |
分析 根据三角形的中位线的性质定理和平行线分线段定理的推论即可判定，根据已知对各个关系式进行分析，从而得到正确的选项．
解答 解：∵AD是△ABC的中线，
∴BD=DC，
∵EF=FC，
∴DF为△CBE的中位线，
∴DF∥BE，
∴△CDF∽△CBE，△AGE∽△ADF
∴GE：DF=AG：AD=1：2，DF：BE=1：2
∴GE：BE=1：4
∴①正确；
连接GF，设BE、DF之间的距离是h，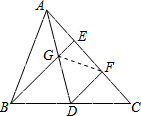
根据题意，得
S△BDG=$\frac{1}{2}$BG•h，S四边形EFDG=S△DFG+S△EGF=$\frac{1}{2}$DF•h+$\frac{1}{2}$EG•h，
又∵DF：BG=2：3，$\frac{1}{2}$DF=GE，
∴S△BDG=$\frac{3}{4}$DF•h，S四边形EFDG=$\frac{3}{4}$DF•h，
∴S△BDG=S四边形EFDG，
∴$\frac{{{S_{△CDF}}}}{{{S_{△BDG}}}}=\frac{2}{3}$．
故选C．
点评 本题考查了三角形中位线定理、平行线分线段成比例定理．解题的关键是证明DF是△CBE的中位线，EG是△ADF的中位线．
练习册系列答案
相关题目
如图，菱形ABCD的对角线长分别为a、b，以菱形ABCD各边的中点为顶点作矩形A1B1C1D1，然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2，…，如此下去，得到四边形A2013B2013C2013D2013的面积用含a、b的代数式表示为$\frac{1}{{2}^{2014}}$ab．
如图，已知圆柱的底面半径为$\frac{6}{π}$cm，高为8cm，蚂蚁从A点爬到B点的最短距离是10cm．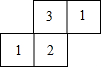
如图是若干个棱长为1cm的正方搭建成的几何体从上面看到的形状图，其中小正方形里的数字表示在该位置小正方体的个数．
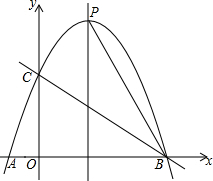如图，抛物线y=ax2+bx+c经过A（-1，0），B（3，0），C（0，3）三点，对称轴与抛物线相交于点P、与直线BC相交于M，连接PB．
