题目内容
1．
如图，已知AP、BP分别平分∠DAB、∠CBA，PM⊥AD于点M，PN⊥BC于点N．求证：点P在线段MN的垂直平分线上．
分析 过点P作PG⊥A于点G，由角平分线的性质可得出PM=PG，PN=PG，故可得出PM=PN，由此可得出结论．
解答 
证明：过点P作PG⊥A于点G，
∵AP、BP分别平分∠DAB、∠CBA，
∴PM=PG，PN=PG，
∴PM=PN，
∴点P在线段MN的垂直平分线上．
点评 本题考查的是线段垂直平分线的性质，熟知垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
相关题目
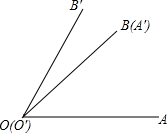如图，将∠A′O′B′的顶点0′和∠A0B的顶点0重合，边0′A与边0B重合，并使两个角的另一边0A和0′B′分别在重合边0B（O′A）的两旁，这时它们不重合的两边组成∠AOB′．那么∠AOB′，∠A0B与∠A′0′B′之间有什么数量关系？
已知：如图，在Rt△ABC中，∠ACB=90°，∠B=60°，CD⊥AB．求证：AB=4DB．
6．2015年国庆期间，我省实现旅游综合收入213.47亿元人民币，这个数据是（ ）
| A． | 精确到0.1 | B． | 精确到0.01 | C． | 精确到千万位 | D． | 精确到百万位 |
如图，A，B，C，D四点在⊙O上，AD平分∠CDE，求证：$\widehat{AB}=\widehat{AC}$．