Question

如图，四边形ABCD内接于⊙O，P、Q、R分别是AB、BC、AD的中点，连接PQ与DA的延长线交于S，连接PR与CB延长线交于T，求证：S、T、Q、R四点共圆．

Answer 1

考点：四点共圆

专题：证明题

分析：连接AC、BD，根据三角形的中位线定理可得PQ∥AC，PR∥BD，根据平行线的性质可得∠PQB=∠ACB，∠ARP=∠ADB，然后根据圆周角定理可得∠ADB=∠ACB，从而得到∠PQB=∠ARP，依据四点共圆的判定定理即可得到S、T、Q、R四点共圆．

解答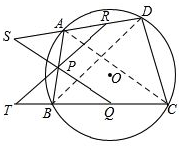：解：连接AC、BD，如图．
∵点P为AB的中点，点Q为BC的中点，点R为AD的中点，
∴PQ∥AC，PR∥BD，
∴∠PQB=∠ACB，∠ARP=∠ADB．
∵∠ADB=∠ACB，
∴∠PQB=∠ARP，
∴S、T、Q、R四点共圆．

点评：本题主要考查了三角形中位线定理、平行线的性质、圆周角定理、四点共圆的判定等知识，由中点联想到三角形中位线定理是解决本题的关键．